В трапеции ABCD точка M – середина боковой стороны CD.

Известно, что ∠DAM=∠MAB=39°.

Найдите угол MBC.

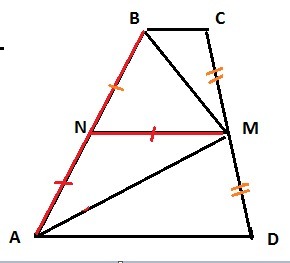
По свойству биссектрис трапеции, AN=NM, значит ∠AMN=39°, тогда ∠MNB=78°-по свойству внешнего угла треугольника. Так как CM=MD-по условию, NM-средняя линия, то NB=AN=NM, ⇒ΔMNB-равнобедренный, ∠NMB=(180-78)/2=51°,  ⇒∠MBC=∠NMB  как накрест лежащие углы при BC║NM и секущей BM.
∠MBC=51°

Есть еще один способ решения найти данный угол, доказав, что BM - биссектриса ∠ABC.