Точка М – середина боковой стороны CD трапеции ABCD.
Площадь треугольника АВМ равна S.
Найдите площадь данной трапеции.

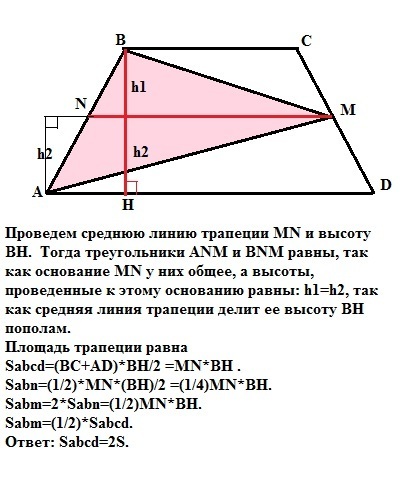
Проведем среднюю линию трапеции MN и высоту ВН.  Тогда треугольники АNM и BNM равны, так как основание MN у них общее, а высоты, проведенные к этому основанию равны: h1=h2, так как средняя линия трапеции делит ее высоту ВН пополам.
Площадь трапеции равна
Sabcd=(BC+AD)*BH/2 =MN*BH .
Sabn=(1/2)*MN*(BH)/2 =(1/4)MN*BH.
Sabm=2*Sabn=(1/2)MN*BH.
Sabm=(1/2)*Sabcd.
Ответ: Sabcd=2S.