OK-биссектриса угла AOB,изображённого на рисунке.Найдите AK,если KB=12, а OA=OB

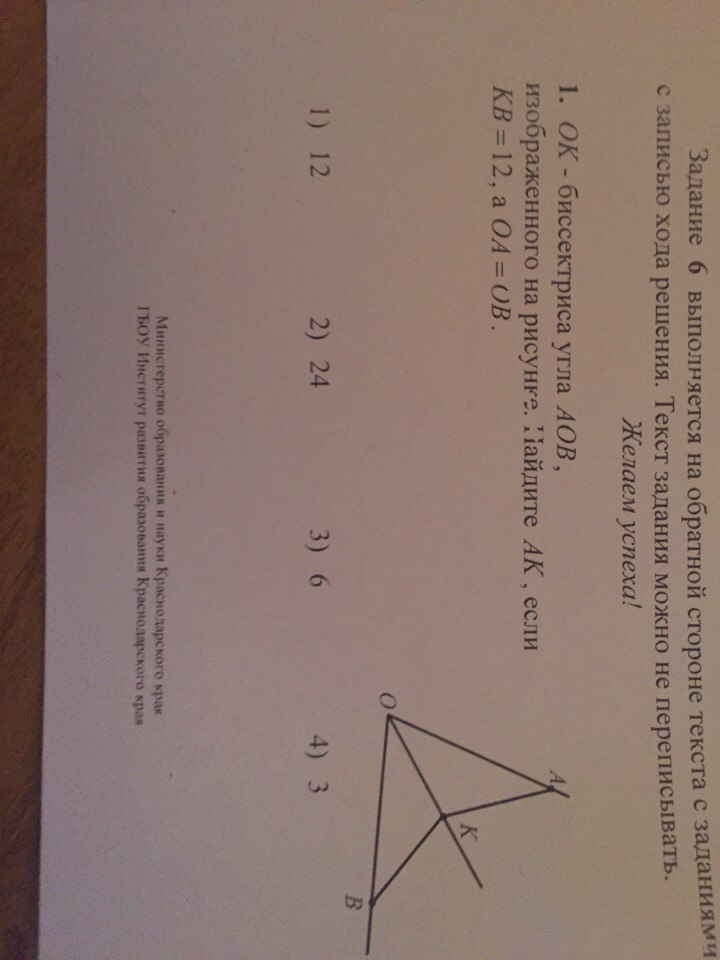
Рассмотрим треугольники АОК и ВОК:
∠АОК = ∠ВОК  (т.к. ОК - биссектриса ∠АОВ)
ОА = ОВ (по условию)
ОК - общая сторона
Следовательно, ΔАОК = ΔВОК по двум сторонам и углу между ними.
В равных треугольниках соответствующие стороны равны, отсюда:
АК = КВ = 12

Ответ: 12

Спасибо)))