Помогите пожалуйста решить
1. Какой многоугольник получится в сечении прямой призмы плоскостью, проходящей через диагональ призмы и её проекцию на основание.
2. ABCD - прямоугольный параллелепипед. Через его диагональ B поведено сечение параллельно прямой A. Найдите площадь этого сечения, если A
3. В наклонной треугольной призме площади двух боковых граней равны 40см и 80см. Угол между ними равен 120. Найдите площадь боковой поверхности призы если длина бокового ребра равна 10 см.

1. В любой прямой призме проекция диагонали призмы на ее основание - диагональ основания. Следовательно, сечение, проходящее через диагональ призмы и её проекцию на основание - это прямоугольник.
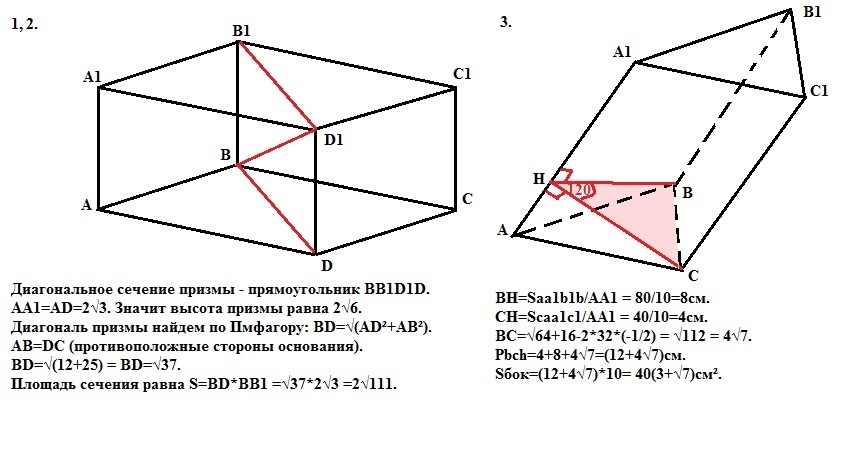
2. Диагональное сечение призмы - прямоугольник ВВ1D1D.
АА1=AD=2√3. Значит высота призмы равна 2√3.
Диагональ призмы найдем по Пифагору: BD=√(AD²+AB²).
АВ=DC (противоположные стороны основания).
BD=√(12+25) = BD=√37.
Площадь сечения равна S=BD*BB1 =√37*2√3 =2√111.
3. Проведем через сторону ВС сечение ВСН, перпендикулярное ребру АА1.Тогда ВН и СН - высоты боковых граней АА1В1В и АА1С1С соответственно и зная площади этих граней, найдем эти высоты.
ВН=Saa1b1b/AA1 = 80/10=8см.
СН=Scaa1c1/AA1 = 40/10=4см.
По теореме косинусов найдем сторону ВС:
ВС=√64+16-2*32*(-1/2) = √112 = 4√7.
Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.
Периметр сечения у нас равен Рbch=4+8+4√7=(12+4√7)см.
Sбок=(12+4√7)*10= 40(3+√7)см².