Братцы ! Помогите хлопцу)
Умоляю, прошу !
Помогите пожалуйста !
Правильное решение !
Заранее огромное спасибо !

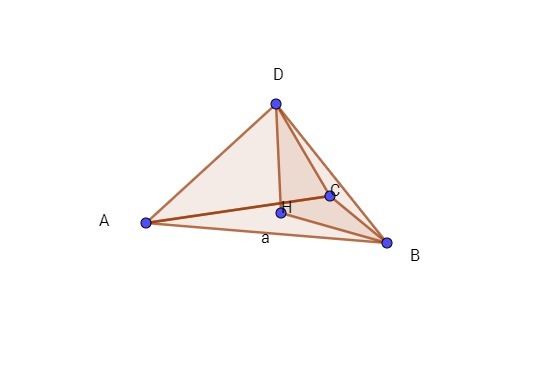
1.найдем сторону AB   равностороннего треугольника ABC , лежащего в основании пирамиды ABCD , она же гипотенуза прямоугольного треугольника ADB  , являющегося боковой гранью пирамиды

AB=√(√48²+√48²)=√96 =4√6

2.  рассмотрим треугольник DBH сторонами которого являются:
 боковое ребро пирамиды  :  BD=√47,
 высота пирамиды DH
 и радиус HB окружности  описанной около равностороннего треугольника,    лежащего в основании пирамиды его находим по формуле R=a*√3/3 
HB = 4√6 *√3/3 =4√18 /3 =12√2 /3 =4√2

данный треугольник является прямоугольным

3. осталось найти DH -  высоту  пирамиды и катет нашего прямоугольного    треугольника DBH

DH =√(√48²- (4√2)²)=√(48- 32) =√16 =4

на калькуляторе не так

√48² =48

лучший !

помоги другие здесь

новые посты сделал

task/26878268
-------------------
Пусть основания ΔABC  , S - вершина пирамиды , SO ⊥ (ABC) .
SA ⊥SB ; SA ⊥SC  ; SB ⊥SC .
L=SA =SB=SC=√48 = 4√3
Пирамида правильная , следовательно  ABC правильный треугольник и высота проходит  через центр основания.
Длина стороны основания a =√(L²+L²) =L√2 =(4√3)*√2 =4√6 ;
Центр основания  точка O совпадает с  точкой пересечения медиан (высот ,  биссектрис ) треугольника  , поэтому
AO=BO =CO =(2/3) *m = (2/3)*(a√3)/2=(a√3)/3 =(4√6 *√3) /3 =4√2.
Высота пирамиды (например из  ΔSOA ):
H = SO =√( L² -AO²) = √( (4√3)² -(4√2)² ) =4√( (√3)² -(√2)² )  =4 .

ответ: 4