Найдите радиус окружности, описанной вокруг прямоугольного треугольника, вершины которого имеют координаты (1;0) (5;6) (10;-6) ответ 6,5, но как решается?

Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, т.е. гипотенуза - диаметр окружности, а радиус - половина гипотенузы.
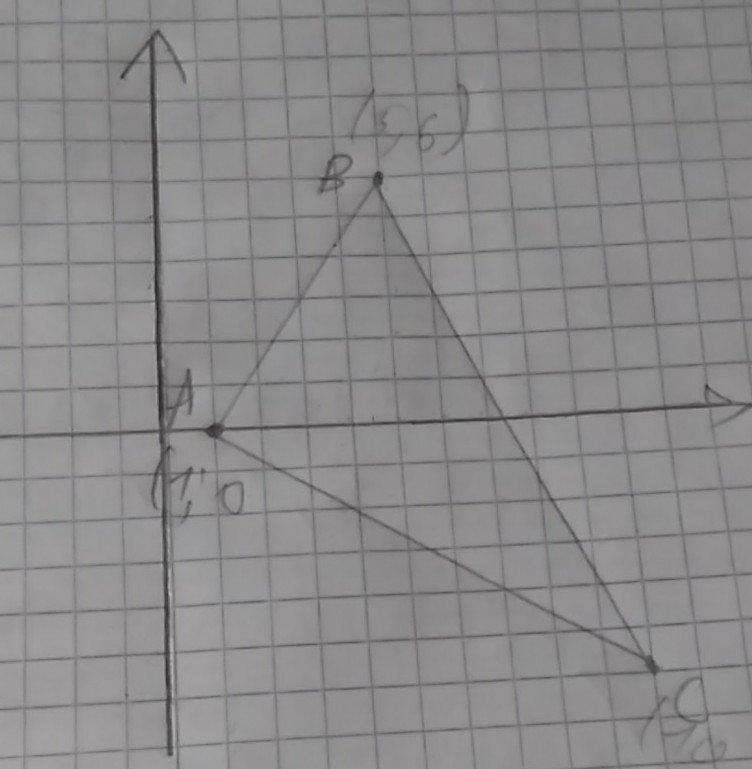
Найдем длину гипотенузы по формуле, предварительно построив треугольник в координатной плоскости:
получается, что длина гипотенузы равна:

Значит, радиус равен 13/2=6,5