Боковая сторона равнобедренного треугольника равна 17 см , а высота треугольника , проведенная к его основанию 15 см . Вычислите площадь данного треугольника . ПОМОГИТЕ ПОЖАЛУЙСТА С РИСУНКОМ !!!!!!

Дано:
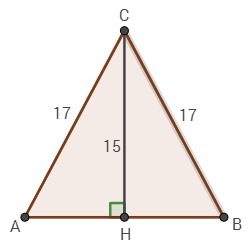
ΔАВС
АС = ВС = 17
СН - высота
СН = 15
Найти: S(ABC)

Из ΔАСН по теореме Пифагора:
  см

В равнобедренном треугольнике высота является также медианой, отсюда:
АВ = 2АН = 2*8 = 16 см

  см²

Ответ: 120 см².