Ответы
Ответ дал:
0
Доказательство:
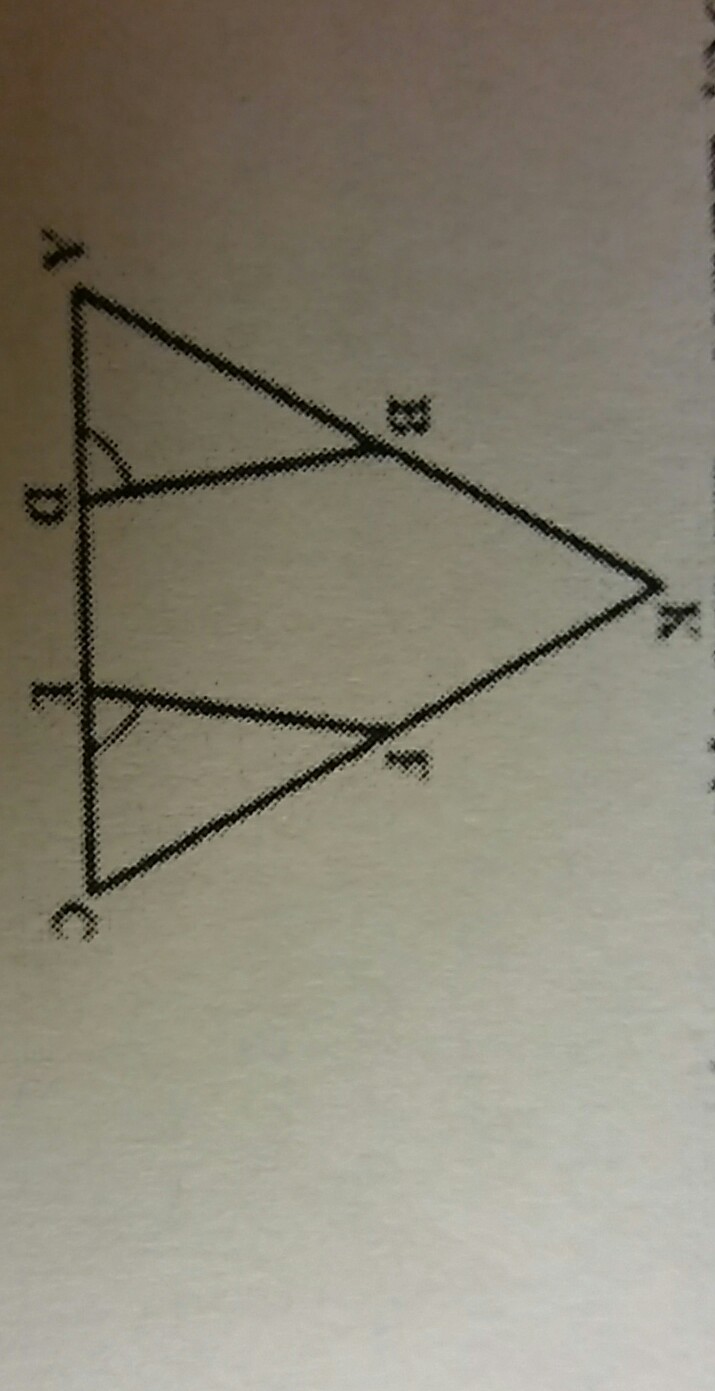
АК = КС = а ⇒ ΔАКС - равнобедренный и ∠ А = ∠С.
АЕ = DC = x - по условию
DE = AE - AD
DE = DC - EC
Приравняем правые части
AE - AD = DC - EC
или
х - АD = x - EC ⇒ AD = EC
ΔABD = ΔCFE по 2-му признаку равенства треугольников (∠BDA = ∠FEC по условию; выше доказано, что ∠А = ∠С и AD = EC)
Из равенства треугольников следует, что АВ = CF = y.
AK = AB + BK и КС = CF + KF
откуда
ВК = АК - АВ и KF = KC - CF
или
ВК = а - у и KF = a - y, то есть ВК = KF, что и требовалось доказать
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
9 лет назад
9 лет назад
9 лет назад
9 лет назад