Предмет: Алгебра
Автор: Аноним
Вопрос задан 8 лет назад

Помогите решить нужно подробное решение

. Даны координаты вершин треугольника А, В, С.
Требуется найти:
1) уравнение и длину стороны ВС;
2) уравнение и длину высоты, проведённой из вершины А;
3) уравнение медианы, проведённой из вершины А;
4) площадь треугольника.
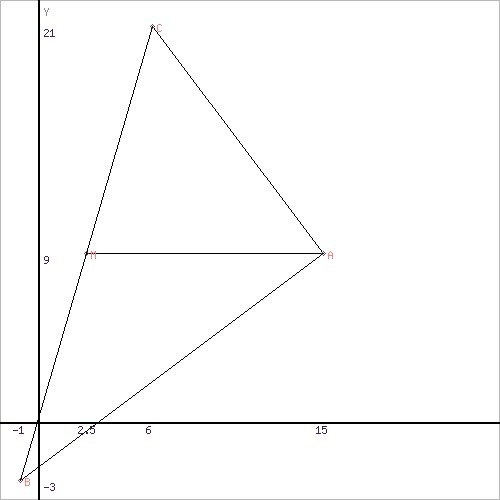
Сделать чертёж.
мои данные
А(15;9), B(-1;-3), C(6;21).

Ответы

Ответ дал: danyaseiy

Вычисление параметров треугольника по координатам его вершинПоложим A(x A ;y A )=A(15;9), B(x B ;y B )=B(−1;−3), C(x C ;y C )=C(6;21).

1) Вычислим длины сторон:

|BC| =√(x C −x B ) ^2 +(y C −y B ) ^2 =√(6−(−1))^ 2 +(21-(−3)) ^2 =√7 ^2 +24^ 2 =√49+576 =√625=√25.

2) Составим уравнения сторон:

BC: x−xB/xC−xB=y−yB/yC−yB ⇔ x−(−1)6−(−1)=y−(−3)21−(−3) ⇔ x+17=y+324 ⇔ 24x−7y+3=0.

6) Вычислим площадь треугольника:

S =1/2 |(x B −x A )(y C −y A )−(x C −x A )(y B −y A )∣ =1/2 ∣(−1−15)(21−9)−(6−15)(−3−9)∣=1/2 ∣(−16)⋅12−(−9)⋅(−12)∣ =12 ∣ −192−108∣=|−300|/2 =300/2 =150.

10) Составим уравнения медиан:

AA1 : x−x A /x A 1 −x A =y−y A /y A 1 −y A ⇔ x−152.5−15 =y−99−9 ⇔ x−15−12.5 =y−90 ⇔ y−9=0.

13) Вычислим длины высот. Пусть A 2 ,B 2 ,C 2 A2,B2,C2 — точки, лежащие на сторонах (или их продолжениях) треугольника, на которые опущены высоты из вершин A,B,C A,B,C соответственно. Тогда, по известной формуле, имеем:

|AA 2 |=2S/|BC| =2⋅150/25 =12;

14) Составим уравнения высот: