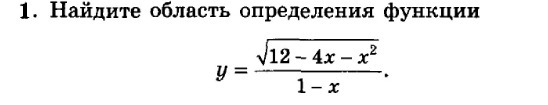Найти область определения. Срочно,с объяснениями,баллы

Подкоренное выражение корня чётной степени должно быть ≥ 0 .
Знаменатель дроби не должен равняться нулю, то есть:
1 - x ≠ 0
x ≠ 1

12 - 4x - x² ≥ 0
x² + 4x - 12 ≤ 0
Найдём корни квадратного трёхчлена и решим неравенство методом интервалов.
x² + 4x - 12 = 0
D = (- 4)² - 4 * 1 * (- 12) = 16 + 48 = 64 = 8²


(x - 2)(x + 6) ≤ 0
        +                  -                     +
_____________________________
              - 6                        2
x ∈ [- 6 ; 2]
Из этого ответа мы должны исключить  x = 1
Окончательный ответ: x ∈ [- 6 ; 1)∪(1 ; 2]

вопрос: почему не взяли промежуток от минус бесконечности до 6,он ведь по знаку отрицателен

все,понял

Он по знаку положителен, а не отрицателен- это видно на рисунке.