В равнобедренном треугольнике к боковой стороне проведена высота и биссектриса угла, прилежащего основанию.

Определите угол между высотой и биссектрисой, если угол вершины ∠B = 32°.

По свойству равнобедренного треугольника ∠А=(180-32)/2=74°,
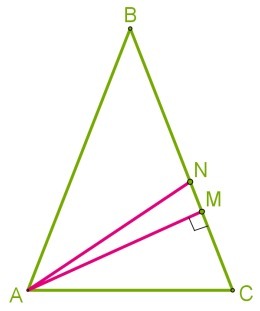
AN-биссектриса ∠А⇒∠ВАN=1/2∠А=74/2=37°, ∠ANB=180-37-32=111°, это внешний угол ΔАNB, значит ∠NAM=111-90=21°