С точки, которая находится на расстоянии 12 см от плоскости, проведено к этой плоскости две наклонные, угол между которыми 90°.
Найдите угол между проекциями наклонных, которые равны 9 см и 16 см.
Помогите, если можно с рисунком

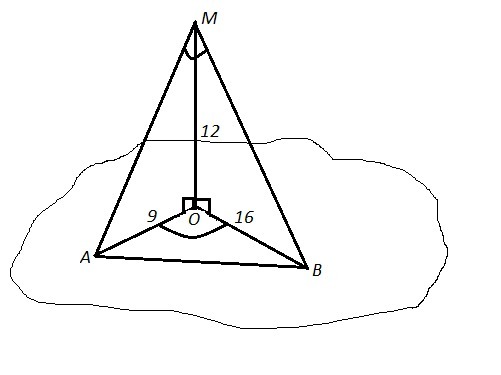
МО⊥пл.α   ⇒  МО⊥АО  и  МО⊥ВО
ΔАОМ и ΔВОМ - прямоугольные
АМ²=АО²+МО²=12²+9²=225=15²  ,  АМ=15
ВМ²=ВО²+ВМ²=16²+12²=400=20²  ,  ВМ=20
∠АМВ=90°  по условию  ⇒  АВ²=ВМ²+АМ²=15²+20²=625=25² , АВ=25
АО+ВО=9+16=25=АВ  ⇒  ∠АОВ=180°
Если не заметить, что АО+ВО=АВ, то чтобы найти ∠АОВ, надо воспользоваться теоремой косинусов в ΔАОВ:
25²=9²+16²-2·9·16·сosα
625=337-288·cosα
288=-288·cosα
cosα=-1  ⇒  α=180°

Браво! Я даже не рассчитывая ничего, почему-то сразу подумал, что обе проекции будут на одной прямой.