Вычислить площадь фигуры, ограниченной линиями у=2х, у=2, х=2

ДАНО
Y = 2/x,
y = 2,
x= 2.
НАЙТИ
S = ? - площадь
РЕШЕНИЕ
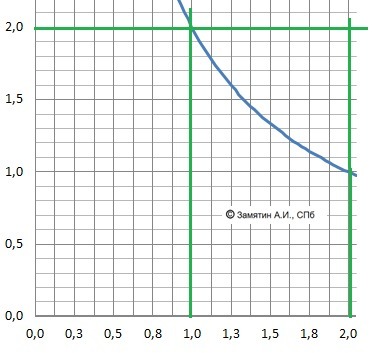
Площадь - интеграл разности функций. Функция У=2 - выше.
Находим пределы интегрирования
a = x = 2 - дано. 
Решаем уравнение
2/х =2 или b = 1
Пишем уравнение для площади фигуры

Вычисляем площадь - разность интегралов
S = 2 - log(4) ≈ 0.614 - ОТВЕТ
Рисунок к задаче в приложении.