Ответы
Ответ дал:
0
неравенство выглядит страшно, но на самом деле просто снимаешь 7 степень и убираешь корни. потом решаешь показательное неравенство
Приложения:
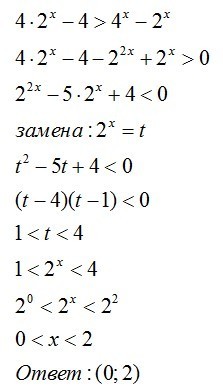
Ответ дал:
0
(x^1/5+2^x+2-2^2)^7>(x^1/5+2^2x-2^x)^7
на 7-ю степень не обращаем внимания,т.к. обе части неравенства в одинаковой степени,тогда
x^1/5+2^x+2-2^2>x^1/5+2^2x-2^x
x^1/5 взаимно уничтожаются,т.к. они противоположные,останется
2^x+2-2^2>2^2x-2^x
в обеих частях неравенства выносим общий множитель с наименьшим показателем степени:
2^2(2^x-1)>2^x(2^x-1)
2^x-1 сокращаются, остается 2^2>2^x
x<2
Неравенству удовлетворяют все числа меньшие 2,т.е.
(-беск;2)
на 7-ю степень не обращаем внимания,т.к. обе части неравенства в одинаковой степени,тогда
x^1/5+2^x+2-2^2>x^1/5+2^2x-2^x
x^1/5 взаимно уничтожаются,т.к. они противоположные,останется
2^x+2-2^2>2^2x-2^x
в обеих частях неравенства выносим общий множитель с наименьшим показателем степени:
2^2(2^x-1)>2^x(2^x-1)
2^x-1 сокращаются, остается 2^2>2^x
x<2
Неравенству удовлетворяют все числа меньшие 2,т.е.
(-беск;2)
Приложения:
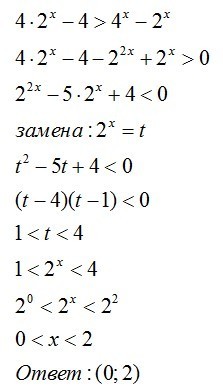
Ответ дал:
0
я нашла ошибку
Ответ дал:
0
Нельзя сокращать на 2^(x-1). Это не число.
Ответ дал:
0
так теряются корни, что и произошло)
Ответ дал:
0
2^2(2^x-1)>2^x(2^x-1); 2^2(2^x-1)-2^x(2^x-1)>0; (2^x-1)* *(2^2-2^x)>0; 2^x-1>0;2^x>2^0; x>0; 2^2-2^x>0; x<2; ответ: (0;2)
Ответ дал:
0
Да)
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
