Предмет: Алгебра
Автор: Fakla
Вопрос задан 8 лет назад

При каких значениях a и b возможно равенство?
sinx=(a+b)/(a-b), где a не равно b.

Ответы

Ответ дал: DNHelper

Синус может изменяться от -1 до 1. Значит, можно составить следующее неравенство:
$-1 leq frac{a+b}{a-b} leq 1 \$
Можно домножить его на a-b, так как условие позволяет. Но нужно следить за знаками:
$left { {{a-b textgreater 0} atop {b-a leq a+b leq a-b}} right. \ left { {{a textgreater b} atop { left { {{a+b geq b-a} atop {a+b leq a-b}} right. }} right. \ left { {{a textgreater b} atop { left { {{a geq 0} atop {b leq 0}} right. }} right.$
На рисунке 1 рассмотрена эта ситуация. Т. е. подходят всё точки в закрашенной области.
Рассмотрим другой случай:
$left { {{a-b textless 0} atop {b-a geq a+b geq a-b}} right. \ left { {{a textless b} atop { left { {{a+b leq b-a} atop {a+b geq a-b}} right. }} right. \ left { {{a textless b} atop { left { {{a leq 0} atop {b geq 0}} right. }} right.$
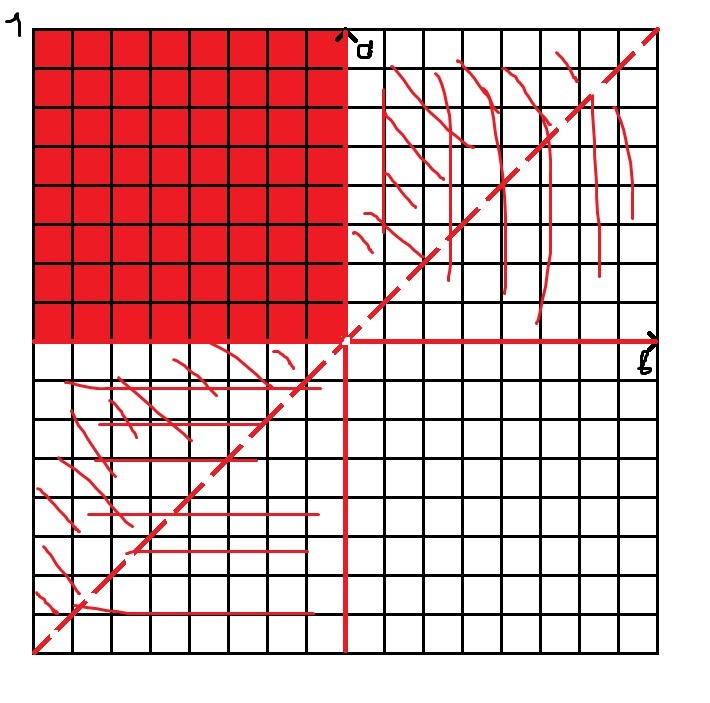
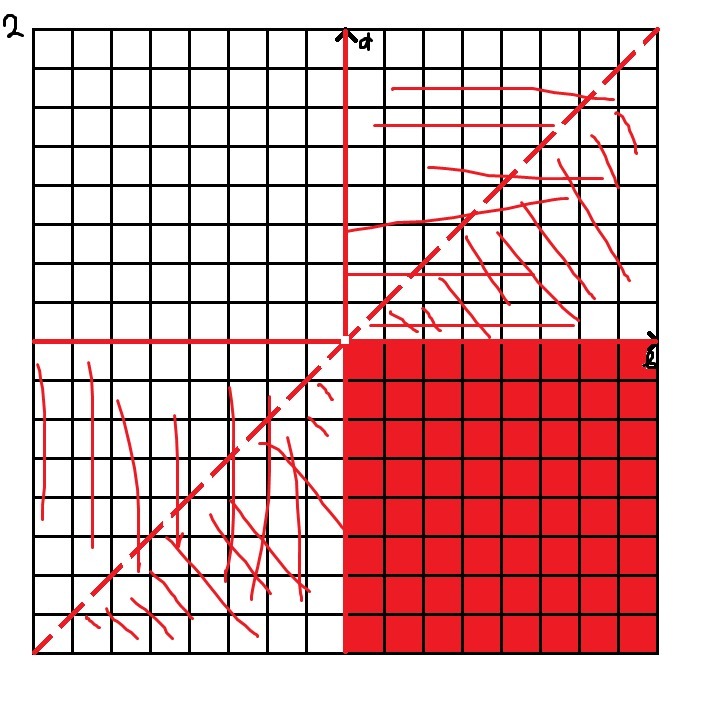
На рисунке 1 рассмотрена эта ситуация. Снова же, подходят всё точки в закрашенной области.

Из этих двух рисунков можно сделать вывод, что равенство возможно в ситуациях, когда a и b имеют разные знаки.

Приложения: