Предмет: Алгебра
Автор: TRENDCAT
Вопрос задан 8 лет назад

Алгебра. Задание по теме пределов. Не могу разобраться с решением пятого задания, помогите.

Приложения:

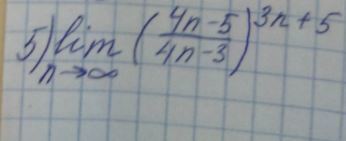
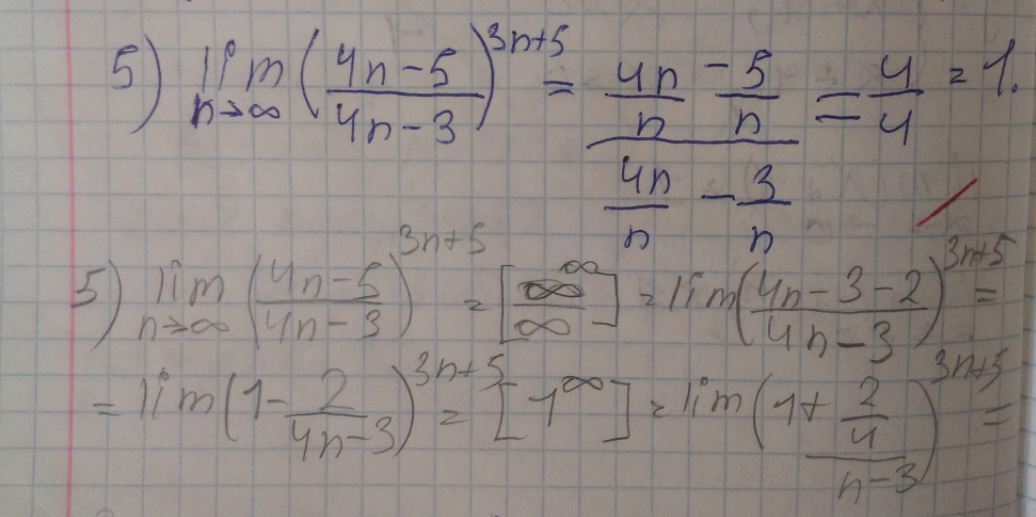
Ответы

Ответ дал: Эксперт5

$lim_{n to infty} ( frac{4n-5}{4n-3})^{3n+5}= lim_{n to infty} ( frac{4n-3-2}{4n-3})^{3n+5}=\\= lim_{n to infty} ( frac{4n-3}{4n-3} + frac{-2}{4n-3} )^{3n+5}= lim_{n to infty}(1+ frac{-2}{4n-3})^{3n+5}}=\\= lim_{n to infty} (1+ frac{1}{ frac{4n-3}{-2} })^{3n+5}=lim_{n to infty} ((1+ frac{1}{ frac{4n-3}{-2} })^{ frac{4n-3}{-2} })^{3n+5}=\\=e^{ lim_{n to infty}{ frac{-2}{4n-3}*(3n+5) } }=e^{-2 lim_{n to infty} frac{3n+5}{4n-3} }=$
$=e^{-2 lim_{n to infty} frac{ frac{3n}{n} + frac{5}{n} }{ frac{4n}{n} - frac{3}{n} } }=e^{-2 lim_{n to infty} frac{3+ frac{5}{n} }{4- frac{3}{n} } } =e^{-2* frac{3}{4} }=e^{- frac{3}{2} }= frac{1}{e sqrt{e} }$

Похожие вопросы

Окружающий мир

2 года назад

в какое время зацветают растения в Арктике?

Русский язык

2 года назад

Что такое фразеолагизмы пожалуйста помогите только в полном ответе

Литература

2 года назад

риси характеру діда Салимона (Тореадори з Васюківки)

Математика

2 года назад