Основание равнобедренного треугольника равно 12 см, а высота, проведенная к
боковой стороне, равна 9,6 см. Найдите периметр треугольника

Дано: ABC - равнобедренный треугольник; AC = 12 см; AD = 9.6 см; AB=BC.

Найти: Рabc.

             Решение:

Из прямоугольного треугольника ADC по теореме Пифагора найдем CD

см.

Пусть , тогда .

Рассмотрим прямоугольный треугольник BHC найдем высоту BH к стороне основания AC; AH=CH=AC/2=6 см.

Площадь равнобедренного треугольника равна , с другой стороны

Приравнивая площади, получим AD * BC = BH * AC.

После возведения в квадрат обе части уравнения и упрощений с подобными членами вы должны получить следующее квадратное уравнение

Корни которого: - не удовлетворяет условию

                                см

Тогда см

Pabc = AB + BC + AC = 10 + 10 + 12 = 32 см

Ответ: 32 см.

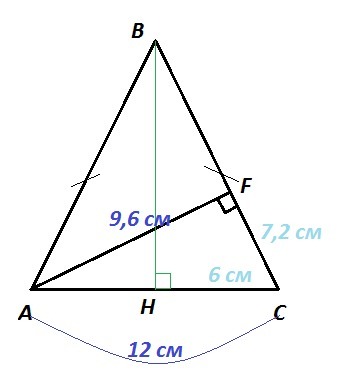
ΔABC - равнобедренный, AB=BC; AF⊥BC; AC=12 см; AF=9,6 см

Найти:

Решение :

ΔAFC - прямоугольный.  По теореме Пифагора

FC² = AC² - AF² = 12² - 9,6² = 51,84 = 7,2²

FC = 7,2 см

Высота BH  в равнобедренном треугольнике, проведенная к основанию AC, является одновременно медианой.  ⇒  

AH = HC = AC/2 = 12/2 = 6 см

ΔAFC ~ ΔBHC. Подобны по двум равным углам:  прямому и общему острому ∠С.

AB = BC = 10 см

Ответ: периметр треугольника равен 32 см