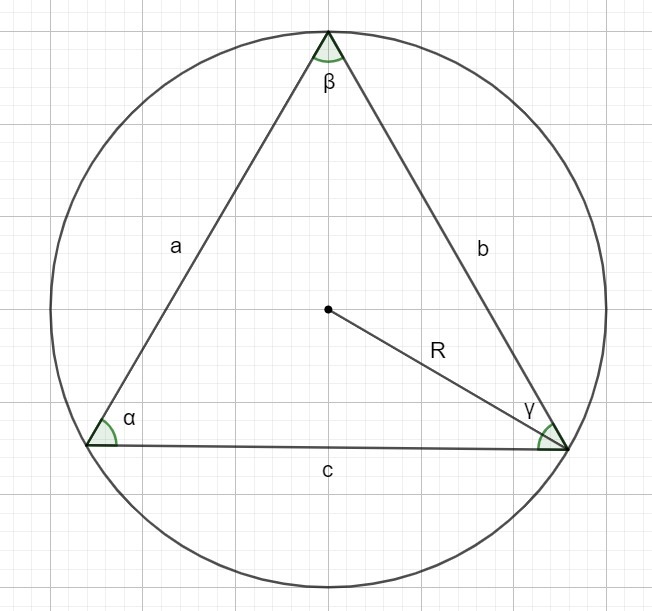
около правильного треугольника описана окружность радиус которой равен 8 см. Найдите а) длину окружности б) периметр треугольника в) площадь треугольника.
Ответы
Ответ дал:
0
Пошаговое объяснение:
R = 8 см.
C - длина окружности, см ?,
P - периметр треугольника, см ?
S - площадь треугольника, см² ?
Определим длину окружности:
С = 2πR = 2π8 = 16π см
Так как треугольник правильный, то
a = b = c
α = β = γ = 60°
Пусть а - сторона правильного треугольника,
тогда исходя из формулы
sin60 = √3/2
а = R * √3 = 8√3 см
Найдем периметр треугольника:
P = 3a = 3 * 8 * √3 = 24√3 см
Найдем площадь правильного треугольника:
см²
Ответ: C = 16π см, P = 24√3 см, S = 48√3 см²
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад