средняя линия равнобедренного треугольника,параллельная основанию, равна 16 см,а биссектриса,проведена к основанию,- 30 см.Найдите среднюю линию,параллельную боковой стороне треугольника.

Вот решение данного задания:

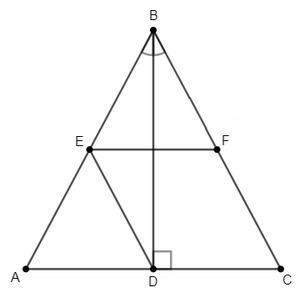
ABC - равнобедренный треугольник, AC - основание.
EF - средняя линия, EF||AC, EF=16 см.
BD - биссектриса, BD=30 см.

Биссектриса к основанию равнобедренного треугольника является также высотой и медианой. BD - биссектриса, следовательно и медиана, а D - середина AC. Отрезок ED соединяет середины сторон AB и AC, является искомой средней линией, параллелен боковой стороне BC и равен ее половине.

ED= BC/2

BD - биссектриса, следовательно и высота, угол BDC - прямой. В прямоугольном треугольнике BDC по теореме Пифагора:

BC=√(BD^2+DC^2)

DC=AC/2 (D - середина AC). Средняя линия EF также равна половине AC, следовательно DC=EF=16 см.

ED =BC/2 =√(BD^2+DC^2)/2 =√(BD^2+EF^2)/2 =
√(30^2 +16^2)/2 =√(15^2 +8^2) =17 (см)