Даю 50 баллов
Напишите плиииз

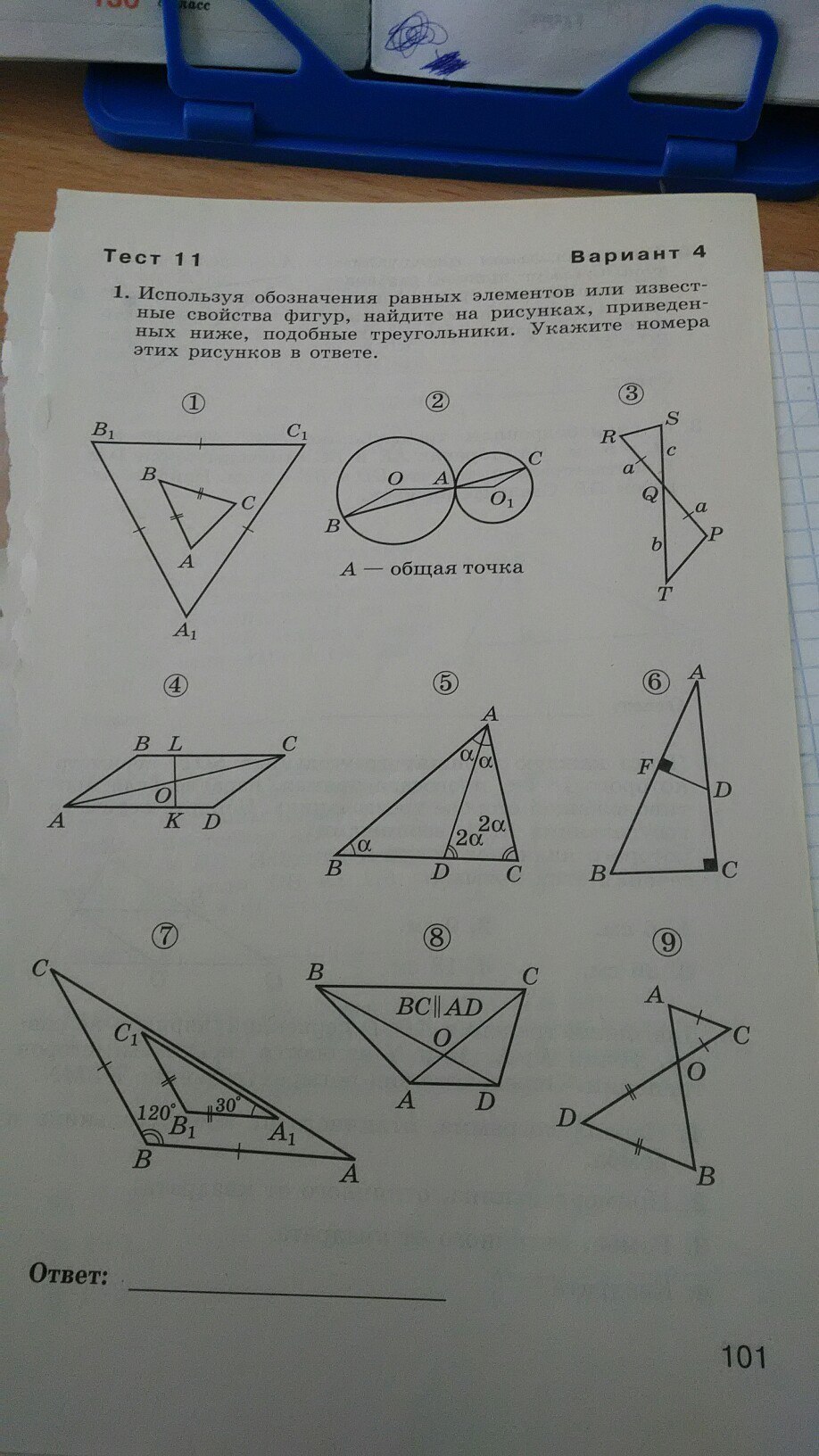
2. ΔBOA ~ ΔCO₁A  
   BO=OA=R ⇒ ΔBOA равнобедренный ⇒  ∠B = ∠OAB
   AO₁=CO₁=r  ⇒  ΔCO₁A  равнобедренный  ⇒ ∠C = ∠CAO₁
  ∠OAB = ∠CAO₁  как вертикальные углы  ⇒
  ΔBOA ~ ΔCO₁A   по двум равным углам при основаниях равнобедренных треугольников

4. Если ABCD - параллелограмм, то 
ΔAOK ~ ΔLOC по двум равным накрест лежащим углам при AD║BC
    Если ABCD - НЕ параллелограмм, то подобных треугольников нет.

5. ΔBAC ~ ΔACD по двум равным углам

6. ΔACB ~ ΔAFD по двум равным углам: прямому и общему ∠А

7. ΔABC ~ ΔA₁B₁C₁  по двум равным углам при основаниях равнобедренных треугольников

8. ΔAOD ~ ΔCOB  по двум равным накрест лежащим углам при BC║AD