Помогите решить 8 задачу,пожалуйста.
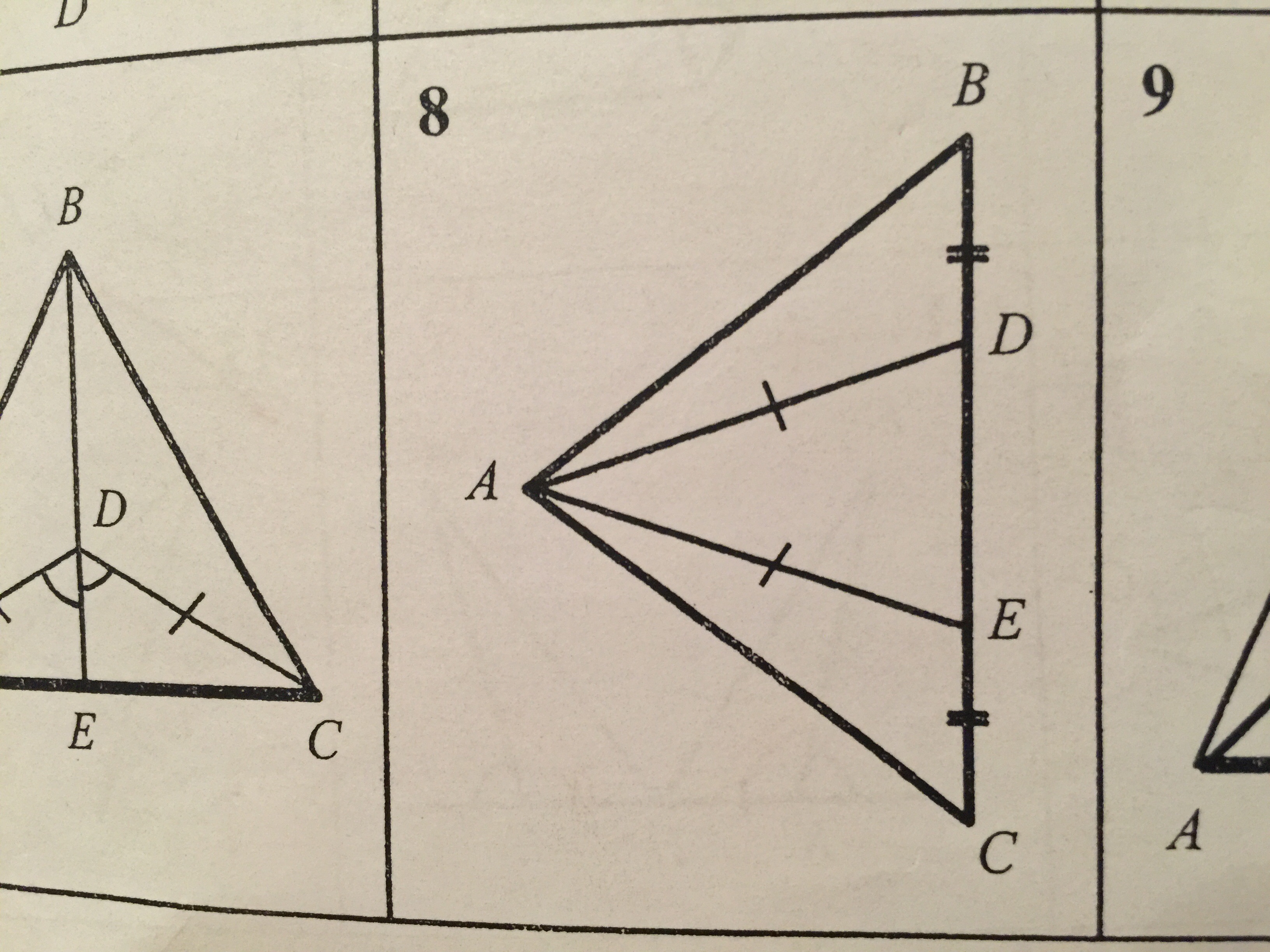
Нужно доказать,что треугольник ABC - равнобедренный.
Приложения:
Ответы
Ответ дал:
2
AD = AE ⇒ ΔEAD - равнобедренный ⇒
∠AED = ∠ADE - как углы при основании
∠AED + ∠AEC = 180° - как смежные углы
∠ADE + ∠ADB = 180° - как смежные углы ⇒
∠AEC = ∠ADB - как углы, смежные к равным углам
Рассмотрим ΔADB и ΔAEC
AD = AE, CE = BD - по условию
∠AEC = ∠ADB ⇒
ΔADB = ΔAEC по двум равным сторонам и углу между ними (первый признак равенства треугольников) ⇒
AB = AC - как стороны равных треугольников, лежащие против равных тупых углов.
AB = AC ⇒ ΔABC - равнобедренный.
Похожие вопросы
1 год назад
1 год назад
1 год назад
2 года назад