у=3х^4-4х^3+2 найти манатоности функции

ДАНО
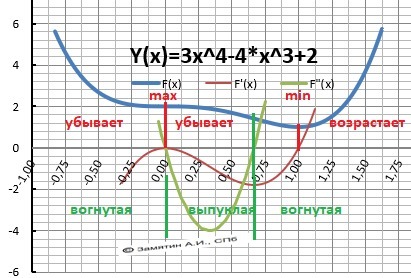
Y(x) = 3*x⁴ -4*x³ + 2
РЕШЕНИЕ
Экстремумы находим по первой производной.
Y'(x) = 12*x³ - 12*x² = 12*x²*(x-1) = 0
Три корня: x₁,₂ = 0, x₃ = 1.
Минимум/максимум -  Y(0) = 2
Минимум - Y(1) = 1.
Интервалы монотонности - ОТВЕТ
Убывает - Х∈(-∞;0]∪[0;1]
Возрастает - Х∈[0;0]∪[1;+∞)
Рисунок с графиком функции в приложении.
Дополнительно на графике - вторая производная и точки перегиба.