Предмет: Геометрия
Автор: Hindexian
Вопрос задан 8 лет назад

100 баллов. Очень СРОЧНО!!! Развернутый ответ с развернутыми вычислениями. С дано, найти и т.п. (Если возможно рисунок). 2 задания.

1) В прямоугольном треугольнике один из катетов равен 5см, гипотенуза 13 см.
Найти:
а) синус острого угла, лежащего против меньшего катета
б) косинус острого угла, лежащего против большего катета
в) тангенс острого угла, лежащего против большего катета.

2) найти sin a, tg a, если cos a=0,25;

Ответы

Ответ дал: xERISx

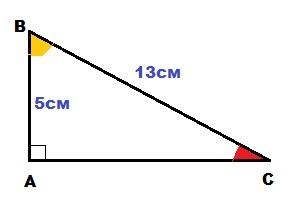
1) Дано: ΔABC : ∠A = 90°; AB = 5 см; BC = 13 см
Найти: sin∠C; cos∠B; tg∠B

Теорема Пифагора
AC² = BC² - AB² = 13² - 5² = 144
AC = √144 = 12 см
AB < AC ⇒ ∠C - меньший острый угол
Формулы соотношений в прямоугольном треугольнике
sin∠C = AB/BC = 5/13
cos∠B = AB/BC = 5/13
tg∠B = AC/AB = 12/5 = 2,4

2) найти sin a, tg a, если cos a=0,25 = $frac{1}{4}$
Основное тригонометрическое тождество
sin²α + cos²α = 1
sin²α = 1 - cos²α = $1 - (frac{1}{4} )^2= 1- frac{1}{16} = frac{15}{16}$
$sin alpha = бsqrt{ frac{15}{16} } =б frac{ sqrt{15} }{4}$

$tg alpha = frac{sin alpha }{cos alpha } = frac{ sqrt{15} }{4} : frac{1}{4} = sqrt{15}$
$tg alpha = frac{sin alpha }{cos alpha } = - frac{ sqrt{15} }{4} : frac{1}{4} =- sqrt{15}$

cos α = 0,25; sin α = 0,25√15; tg α = √15
или
cos α = 0,25; sin α = -0,25√15; tg α = -√15

Приложения: