Найдите радиус окружности, описанной около трапеции с основаниями 12 см и 24 см и боковой стороной 6√10 см

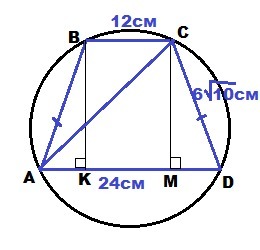
Трапеция ABCD:  BC║AD;  BC = 12 см;  AD = 24 см
Описать окружность можно только около равнобедренной трапеции  ⇒
AB = CD = 6√10  см
Провести две высоты BK⊥AD и CM⊥AD:
KM = BC = 12 см
AK = MD = (AD - KM)/2 = (24 - 12)/2 = 6 см

ΔCMD:  ∠CMD = 90°; MD = 6 см; CD = 6√10 см. Теорема Пифагора
CM² = CD² - MD² = (6√10)² - 6² = 360 - 36 = 324
CM = √324 = 18 см

ΔACM: ∠AMC = 90°;  CM = 18 см;  AM = 6+12 = 18 см  ⇒ 
CM = AM ⇒   ∠CAM = ∠ACM = 90°/2 = 45°

Окружность, которая описана около трапеции, описана и около ΔACD.
Теорема синусов:


Ответ: радиус описанной окружности  равен 6√5 см