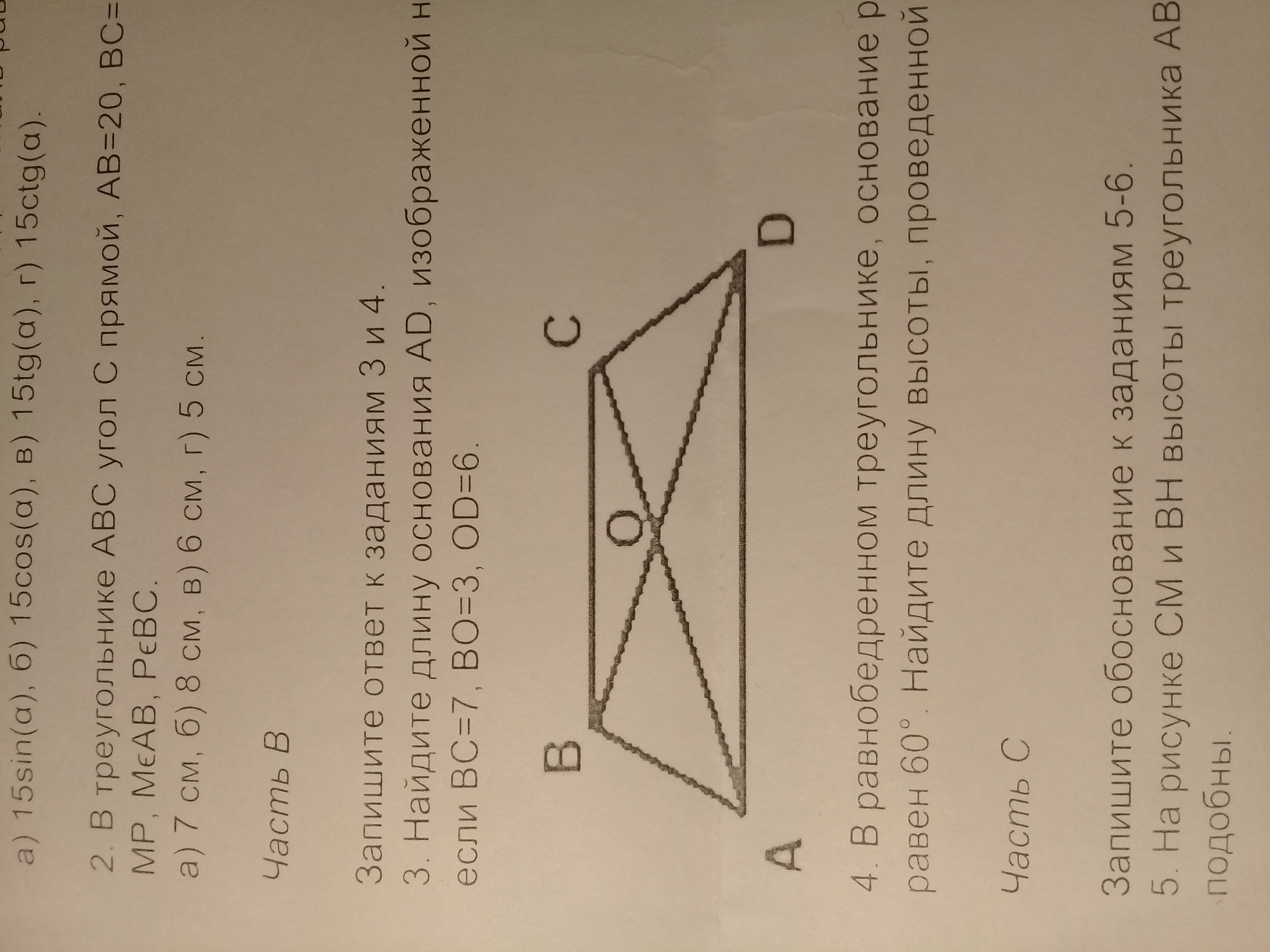
Найдите длину основания AD, изображенной на рисунке трапеции ABCD, если ВC=7,BO=3, OD=6.

∠CBO = ∠ODA - накрест лежащие углы при BC║AD и секущей BD.
∠BOC = ∠DOA - вертикальные углы.

Рассмотрим ΔOBC и ΔOAD:
1. ∠CBO = ∠ODA
2. ∠BOC = ∠DOA
Следовательно, треугольника OBC и ODA подобны.

Из подобия верно:
BC : AD = BO : OD
Откуда AD = BC * OD : BO = 7 * 6 : 3 = 42 : 3 = 14

Ответ: 14