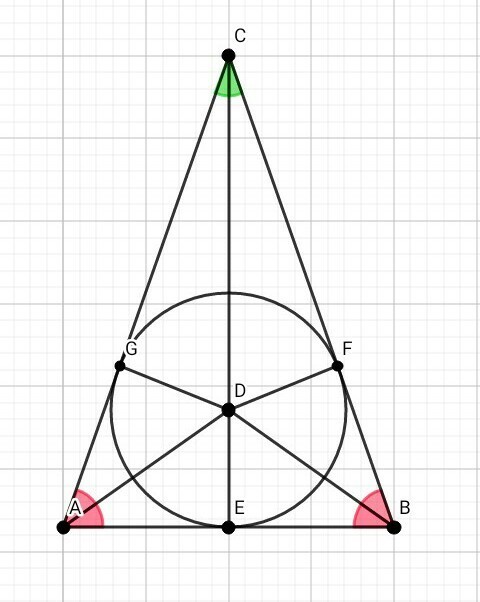
Центр окружности, вписанной в равнобедренный треугольник, делит высоту, проведенную к основанию, на отрезки 5 см и 13 см. Найдите периметр треугольника.

1) CD = 13 см
DE = r = 5 см

DG = DE = DF = 5 см – как радиусы вписанной окружности

Рассмотрим ∆ CDF (угол CFD = 90°):
По теореме Пифагора:
CD² = DF² + CF²
CF² = 13² - 5² = 169 - 25 = 144
CF = 12 см

2) Рассмотрим ∆ CBE (угол СЕВ = 90°):
По теореме касательных к окружности, проведённых из одной точки
BD – биссектриса угла ABC

По свойству биссектрисы:
Биссектриса делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам →

CD/ DE = CB/ BE = 13 / 5

Пусть FB = BE = x , как отрезки кательных к окружности, проведённых из одной точки →

CB / BE = 13 / 5

( 12 + x ) / x = 13 / 5

13x = 5 × ( 12 + x )
13x = 60 + 5x
13x – 5x = 60
8x = 60
x = 60/8 = 7,5 см

Значит, FB = BE = 7,5 см

По свойству отрезков касательных, проведённых из одной точки →

CG = CF = 12 см
GA = AE = 7,5 см

P abc = AC + CB + AB = 12 + 7,5 + 12 + 7,5 + 7,5 + 7,5 = 24 + 30 = 54 см

ОТВЕТ: P abc = 54 см.