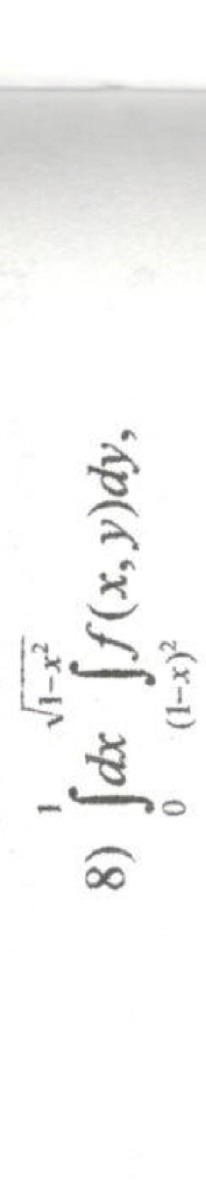Изменить порядок интегрирования. Задание прикрепила. Решите плизз❤️ дам 100 баллов)

Изменить порядок интегрирования в двукратном интеграле это значит преобразовать данный интеграл так, чтобы внешний интеграл зависил от переменной у, а внутренний интеграл зависит от переменной х.

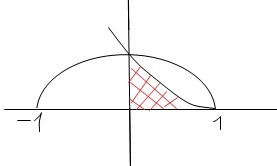
Область интегрирования:

D: 0 ≤ x ≤ 1 - изменение переменной х.
     √(1-x²) ≤ y ≤ (1-x)² - изменение переменной у.

y = √(1-x²)   ⇔   y² = 1- x²  ⇔  x² + y² = 1 - уравнение окружности с центром (0;0) и радиусом R = 1 и при этом y ≥ 0.

а не подскажете, как [tex] на наш язык перевести?

просто затрудняюсь последний абзац прочитать

С браузера зайдите