Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB,если AF=24,BF=7. Помогите Пж очень нужно!!!
Ответы
Ответ дал:
0
Хорошо бы знать, что биссектрисы углов при боковых сторонах трапеции взаимно перпендикулярны. В п.1 и п.2 доказательство этого факта
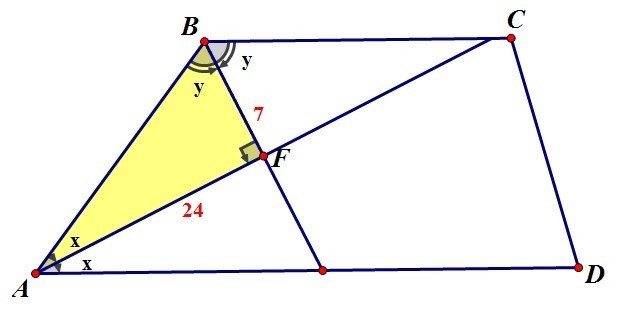
1) Так как сумма углов при боковых сторонах трапеции равна 180°, то ∠А+∠В=2х+2у=180 ⇒х+у=90.
2) Так как сумма двух углов в треугольнике ABF равна 90°, значит, третий угол AFB равен 90°. Получаем, что треугольник ABF - прямоугольный.
3) По теореме Пифагора имеем: AB²=AF²+BF² =576+49=625, Отсюда АВ=25
1) Так как сумма углов при боковых сторонах трапеции равна 180°, то ∠А+∠В=2х+2у=180 ⇒х+у=90.
2) Так как сумма двух углов в треугольнике ABF равна 90°, значит, третий угол AFB равен 90°. Получаем, что треугольник ABF - прямоугольный.
3) По теореме Пифагора имеем: AB²=AF²+BF² =576+49=625, Отсюда АВ=25
Приложения:
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад