ДАМ 40 БАЛЛОВ! Напишите теорему и доказательство о центре окружности, описанной около треугольника. (Доказательство желательно с Дано)

Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон. 

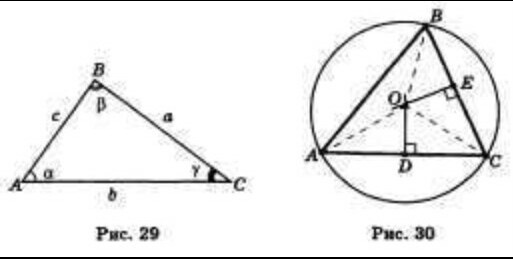
Дано: АВС — данный треугольник; О — центр описанной около него окружности 

Доказательство: Треугольник АОС равнобедренный: у него стороны О А и ОС равны как радиусы. Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне АС и проходящей через ее середину. Точно так же доказывается, что центр окружности лежит на перпендикулярах к двум другим сторонам треугольника. 

Замечание. Прямую, проходящую через середину отрезка перпендикулярно к нему, часто называют серединным перпендикуляром. В связи с этим иногда говорят, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.

почитай после дано

Я вижу, но всегда нужно что - то доказать, а потом уже доказательство

этого я не знаю

простите

Найти надо R-окружности