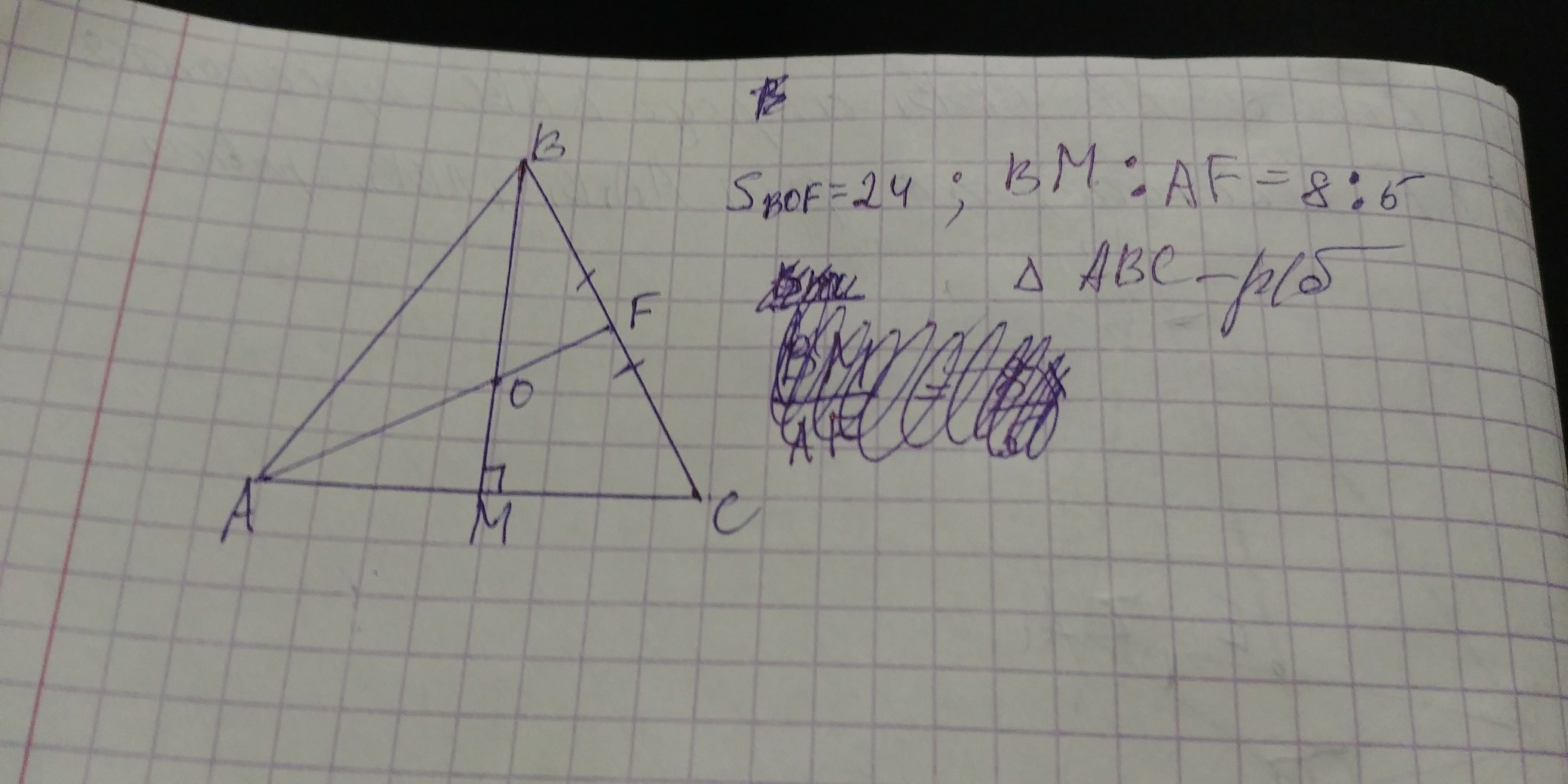
В равнобедренном треугольнике ABC(AB=BC) высота BM пересекает медиану AF в точке О. BM относится к AF как 8 к 5. Площадь треугольника BOF равна 24

т.к. BMпересекаетAF, уголBOF=углуAOM;
т.к. катет углаAOM=90°, треугольники прямоугольные. (BM в 1.6 раз больше AF)
S=(a*b) /2=24; a*b=48; предположим 48*1.6=30; 48-30=15, значит OF=15,
а BO=30.
BF²=BO²/OF²
BF²=900/225
BF²=4
BF=2
Я не опытный, это лишь теории, но может чем-то поможет.

Хотя и так может быть, ведь рисунок не всегда правильный. Может BO < OF