ребята очень срочно решите задачи по алгебре номер 30. задания:1,3,6,9,11,13. ПОЖАЙЛУСТААА! !!
Приложения:
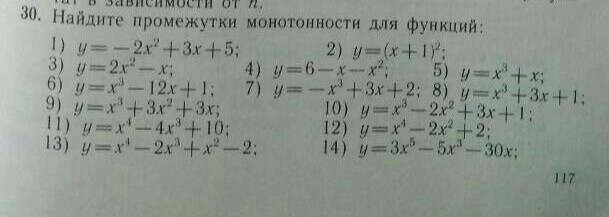
Ответы
Ответ дал:
0
1) y = - 2x² + 3x + 5
Найдём производную
y' = - 2(x²)' + 3(x)' + 5' = - 4x + 3
Приравняем производную к нулю
y' = 0 ⇒ - 4x + 3 = 0 ⇒ x = 0,75
Отметим эту точку на числовой прямой и вычислим знаки производной в каждом из двух промежутков:
+ -
____________________
0,75
max
Значит на промежутке (- ∞ ; 0,75] - функция возрастает , а на промежутке [0,75 ; + ∞) - убывает
Точка x = 0,75 - это точка максимума так как при переходе через эту точку производная меняет знак с "+" на "-" .
Итак y(0,75) - это max
Найдём значение функции в точке максимума
y(0,75) = - 2 * 0,75² + 3 * 0,75 + 5 = -1,125 + 2,25 + 5 = 6,125
Следующие задания решу без объяснения, так как они аналогичны.
3) y = 2x² - x
y' = 2(x²)' - x' = 4x - 1
y' = 0 ⇒ 4x - 1 = 0 ⇒ x = 0,25
- +
_______________________
0,25
min
На промежутке (- ∞ ; 0,25] - убывает , на прмежутке [0,25 ; + ∞) - возрастает.
x = 0,25 - точка минимума так как при переходе через эту точку производная меняет знак с "-" на "+" .
y(0,25) = 2 * 0,25² - 0,25 = 0,125 - 0,25 = - 0,125 - значение функции в точке минимума.
6) y = x³ - 12x + 1
y' = (x³)' - 12(x)' + 1' = 3x² - 12
y' = 0 ⇒ 3x² - 12 = 0 ⇒ x² - 4 = 0 ⇒ (x - 2)(x + 2) = 0
x - 2 = 0 ⇒ x = 2
x + 2 = 0 ⇒ x = - 2
+ - +
_______________________________
- 2 2
max min
(- ∞ ; - 2 ] и [2 ; + ∞) - возрастает
[ - 2 ; 2 ] - убывает
x = - 2 - точка максимума
x = 2 - точка минимума
y( - 2 ) = (-2)³ - 12 * (- 2) + 1 = - 8 + 24 + 1 = 17
y(2) = 2³ - 12 * 2 + 1 = 8 - 24 + 1 = - 15
9) y = x³ + 3x² + 3
y' = (x³)' + 3(x²)' + 3' = 3x² + 6x
y' = 0 ⇒ 3x² + 6x = 0 ⇒ x² + 2x = 0 ⇒ x(x + 2) = 0 ⇒ x = 0 , x = - 2
+ - +
____________________________
- 2 0
max min
(- ∞ ; - 2] и [0 ; + ∞) - возрастает
[- 2 ; 0] - убывает
x = - 2 - точка максимума
x = 0 - точка минимума
y( - 2) = (- 2)³ + 3 * (- 2)² + 3 = - 8 + 12 + 3 = 7
y ( 0) = 0³ + 3 * 0² + 3 = 3
11) y = x⁴ - 4x³ + 10
y' = (x⁴)' - 4 (x³)' + 10' = 4x³ - 12x²
y' = 0 ⇒ 4x³ - 12x² = 0 ⇒ x³ - 3x² = 0 ⇒ x²(x - 3) = 0 ⇒ x = 0 , x = 3
- - +
________________________________
0 3
min
(- ∞ ; 3] - убывает , [3 , + ∞) - возрастает
x = 3 - точка минимума
y(3) = 3⁴ - 4 * 3³ + 10 = 81 - 108 + 10 = - 17
13) y = x⁴ - 2x³ + x² - 2
y' = (x⁴)' - 2(x³)' + (x²)' - 2' = 4x³ - 6x² + 2x
y' = 0 ⇒ 4x³ - 6x² + 2x = 0 ⇒ 2x³ - 3x² + x = 0 ⇒ x(2x² - 3x + 1) = 0
x = 0 2(x - 1)(x - 0,5) = 0 ⇒ x = 1 , x = 0,5
- + - +
__________________________________
0 0,5 1
min max min
(- ∞ ; 0] и [0,5 ; 1] - убывает
[0 , 0,5] и [1 ; + ∞) - возрастает
x = 0 и x = 1 - точки минимума
x = 0,5 - точка максимума
y( 0) = 0⁴ - 2 * 0³ + 0² - 2 = - 2
y(0,5) = 0,5⁴ - 2 * 0,5 ³ + 0,5 ² - 2 = 0,0625 - 0,25 + 0,25 - 2 = - 1,9375
y(1)= 1⁴ - 2 * 1³ + 1² - 2 = 1 - 2 + 1 - 2 = - 2
Найдём производную
y' = - 2(x²)' + 3(x)' + 5' = - 4x + 3
Приравняем производную к нулю
y' = 0 ⇒ - 4x + 3 = 0 ⇒ x = 0,75
Отметим эту точку на числовой прямой и вычислим знаки производной в каждом из двух промежутков:
+ -
____________________
0,75
max
Значит на промежутке (- ∞ ; 0,75] - функция возрастает , а на промежутке [0,75 ; + ∞) - убывает
Точка x = 0,75 - это точка максимума так как при переходе через эту точку производная меняет знак с "+" на "-" .
Итак y(0,75) - это max
Найдём значение функции в точке максимума
y(0,75) = - 2 * 0,75² + 3 * 0,75 + 5 = -1,125 + 2,25 + 5 = 6,125
Следующие задания решу без объяснения, так как они аналогичны.
3) y = 2x² - x
y' = 2(x²)' - x' = 4x - 1
y' = 0 ⇒ 4x - 1 = 0 ⇒ x = 0,25
- +
_______________________
0,25
min
На промежутке (- ∞ ; 0,25] - убывает , на прмежутке [0,25 ; + ∞) - возрастает.
x = 0,25 - точка минимума так как при переходе через эту точку производная меняет знак с "-" на "+" .
y(0,25) = 2 * 0,25² - 0,25 = 0,125 - 0,25 = - 0,125 - значение функции в точке минимума.
6) y = x³ - 12x + 1
y' = (x³)' - 12(x)' + 1' = 3x² - 12
y' = 0 ⇒ 3x² - 12 = 0 ⇒ x² - 4 = 0 ⇒ (x - 2)(x + 2) = 0
x - 2 = 0 ⇒ x = 2
x + 2 = 0 ⇒ x = - 2
+ - +
_______________________________
- 2 2
max min
(- ∞ ; - 2 ] и [2 ; + ∞) - возрастает
[ - 2 ; 2 ] - убывает
x = - 2 - точка максимума
x = 2 - точка минимума
y( - 2 ) = (-2)³ - 12 * (- 2) + 1 = - 8 + 24 + 1 = 17
y(2) = 2³ - 12 * 2 + 1 = 8 - 24 + 1 = - 15
9) y = x³ + 3x² + 3
y' = (x³)' + 3(x²)' + 3' = 3x² + 6x
y' = 0 ⇒ 3x² + 6x = 0 ⇒ x² + 2x = 0 ⇒ x(x + 2) = 0 ⇒ x = 0 , x = - 2
+ - +
____________________________
- 2 0
max min
(- ∞ ; - 2] и [0 ; + ∞) - возрастает
[- 2 ; 0] - убывает
x = - 2 - точка максимума
x = 0 - точка минимума
y( - 2) = (- 2)³ + 3 * (- 2)² + 3 = - 8 + 12 + 3 = 7
y ( 0) = 0³ + 3 * 0² + 3 = 3
11) y = x⁴ - 4x³ + 10
y' = (x⁴)' - 4 (x³)' + 10' = 4x³ - 12x²
y' = 0 ⇒ 4x³ - 12x² = 0 ⇒ x³ - 3x² = 0 ⇒ x²(x - 3) = 0 ⇒ x = 0 , x = 3
- - +
________________________________
0 3
min
(- ∞ ; 3] - убывает , [3 , + ∞) - возрастает
x = 3 - точка минимума
y(3) = 3⁴ - 4 * 3³ + 10 = 81 - 108 + 10 = - 17
13) y = x⁴ - 2x³ + x² - 2
y' = (x⁴)' - 2(x³)' + (x²)' - 2' = 4x³ - 6x² + 2x
y' = 0 ⇒ 4x³ - 6x² + 2x = 0 ⇒ 2x³ - 3x² + x = 0 ⇒ x(2x² - 3x + 1) = 0
x = 0 2(x - 1)(x - 0,5) = 0 ⇒ x = 1 , x = 0,5
- + - +
__________________________________
0 0,5 1
min max min
(- ∞ ; 0] и [0,5 ; 1] - убывает
[0 , 0,5] и [1 ; + ∞) - возрастает
x = 0 и x = 1 - точки минимума
x = 0,5 - точка максимума
y( 0) = 0⁴ - 2 * 0³ + 0² - 2 = - 2
y(0,5) = 0,5⁴ - 2 * 0,5 ³ + 0,5 ² - 2 = 0,0625 - 0,25 + 0,25 - 2 = - 1,9375
y(1)= 1⁴ - 2 * 1³ + 1² - 2 = 1 - 2 + 1 - 2 = - 2
Ответ дал:
0
большое спасибо тебе универсалочка!
Ответ дал:
0
Всегда пожалуйста)
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад