помогите решить,пожалуйста

По определению первообразной на интервале (−3; 5) справедливо равенство

f(x)=F'(x).

 

Следовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −2,6; −2,2; −1,2; −0,5; 0; 0,4; 0,8; 1,2; 2,2; 2,8; 3,4; 3,8. Из них на отрезке [−2;4] лежат 10 точек. Таким образом, на отрезке [−2;4] уравнение f(x)=0 имеет 10 решений.

 

Ответ: 10.

это 1.


разность значений первообоазной в точках 8 и 2 равна площади выделенной на рисунке трапеции ABCD Поэтому

f(b) - F(a)=1+6/2•2=7

 

Ответ:7.

фух. надеюсь правильно))

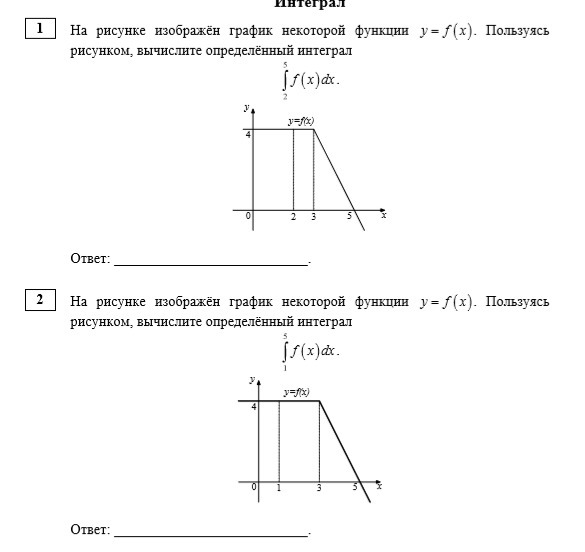
  Значение определённого интеграла равно площади криволинейной трапеции, ограниченной функцией у=f(x) , х=а , x=b , у=0 .
1)  Вычислим площадь криволинейной трапеции, которая на самом деле явл. трапецией с основаниями , равными 3 и 5, высотой, равной 4 :
 S=(3+5)/2*4=16 .
                               
2) Трапеция с основаниями 3 и 5 и высотой 4:  S=(3+5)/2*4=16 .