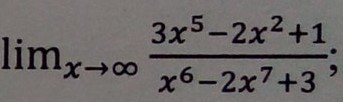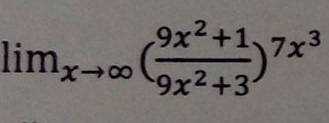Ответы
Ответ дал:
0
1)
Мы видим ,что сократятся и в числители и в знаменателе
сократятся и в числители и в знаменателе
Потом мы вместо "х" подставим "∞" и получи
Так как мы делим число на бесконечность по правилу получаем "0"
2)Мы выносим "7" так как она нам не нужно и это константа

Аналогично ,как и в первой задачи мы должны вынести "х" и сократить (сразу сделаем)


И только теперь можно подставить "∞" и получаем ,в числители "∞" ,в знаменателе "9". Делим и получаем. Ответ :∞
Мы видим ,что
Потом мы вместо "х" подставим "∞" и получи
Так как мы делим число на бесконечность по правилу получаем "0"
2)Мы выносим "7" так как она нам не нужно и это константа
Аналогично ,как и в первой задачи мы должны вынести "х" и сократить (сразу сделаем)
И только теперь можно подставить "∞" и получаем ,в числители "∞" ,в знаменателе "9". Делим и получаем. Ответ :∞
Ответ дал:
0
Спасибо большое еще раз)
Похожие вопросы
2 года назад
2 года назад
8 лет назад
9 лет назад