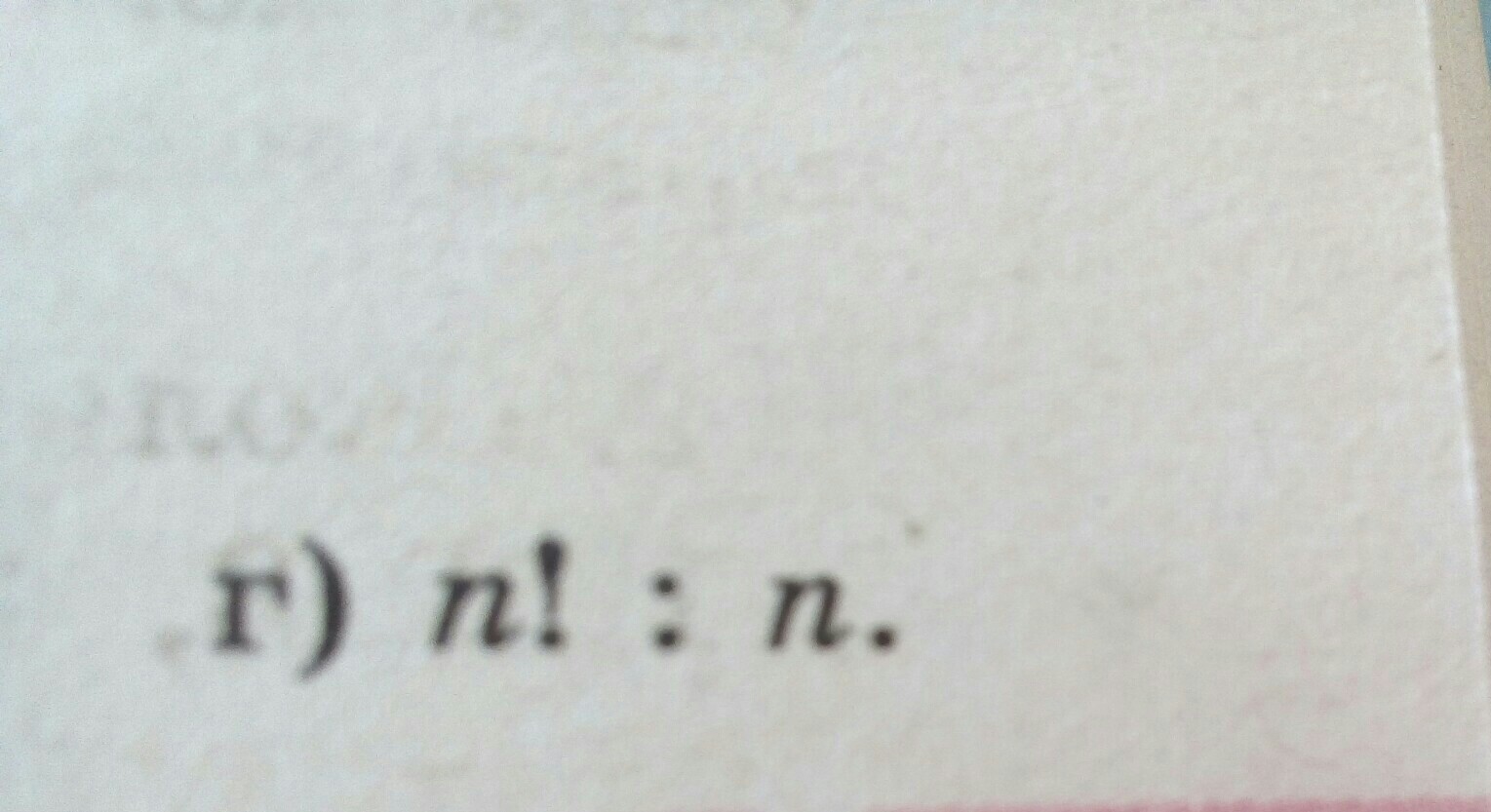Предмет: Алгебра
Автор: bertain
Вопрос задан 8 лет назад

100 баллов. Решить факториал. С объяснением

Приложения:

Ответы

Ответ дал: AnonimusPro

определение факториала:
$n!=1*2*3*...*(n-1)*n \0!=1$
нужно упростить выражение:
$frac{n!}{n}$
преобразуем числитель:
$n!=1*2*3*...*(n-1)*n=(1*2*3*...*(n-1))*n$
по определению факториала:
$1*2*3*...*(n-1)=(n-1)!$
значит:
$n!=1*2*3*...*(n-1)*n=(1*2*3*...*(n-1))*n=\=(n-1)!*n$
подставим в дробь и сократим:
$frac{n!}{n}= frac{n(n-1)!}{n} =(n-1)!$
Ответ: (n-1)!

Ответ дал: vvbarashovsky

n!n=(n-1)!*nn ясно что n=1 , 2 ,3 ....... натуральные числа n не равно нулю

(n-1)!*nn=(n-1)! - это и есть ответ

Похожие вопросы

Русский язык

2 года назад

Мне нужно 5 предложений с глаголами

Русский язык

2 года назад

Сделать полный синтаксический разбор предложения. Вы,наверное,знаете задание строящееся нами.

Английский язык

2 года назад

Срочно английский язык 4 класс!!! Homework