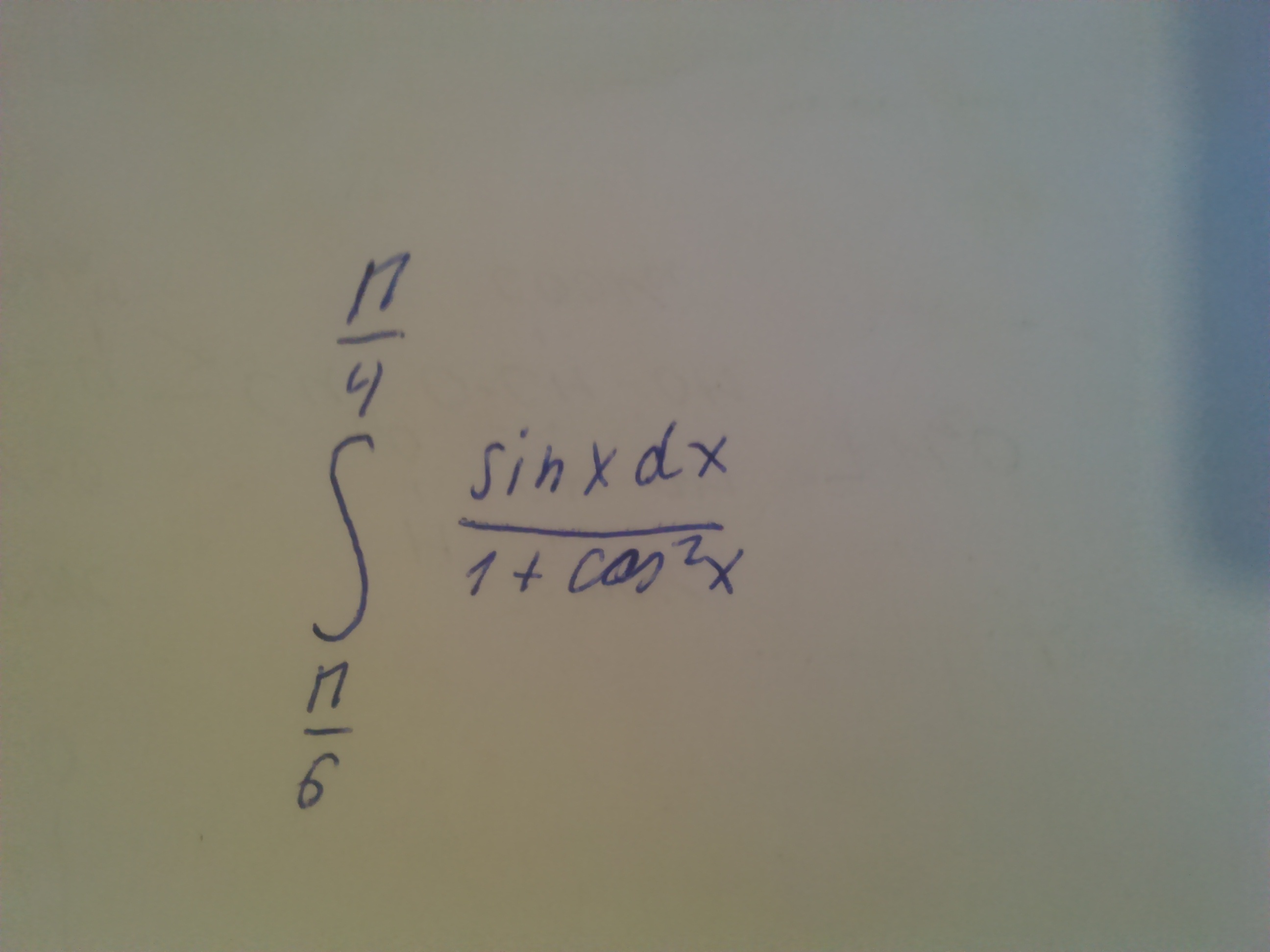Ответы
Ответ дал:
0
интеграл (π/6 до π/4)sinx/(1+cos²x)dx=
интег(π/6 до π/4)-(d(cosx)/(1+cos²x)=
-(arctg(cosx))(π/6 π/4)=
-(arctg(cosπ/4)-arctg(cosπ/6)=
arctg(√3/2)-arctg(√2/2)
(arctgf(x))'=1/(1+f²(x))*(f'(x))
интег(π/6 до π/4)-(d(cosx)/(1+cos²x)=
-(arctg(cosx))(π/6 π/4)=
-(arctg(cosπ/4)-arctg(cosπ/6)=
arctg(√3/2)-arctg(√2/2)
(arctgf(x))'=1/(1+f²(x))*(f'(x))
Ответ дал:
0
спасибо большое
Похожие вопросы
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад