Нужно решение двух задач с чертежом. Номер 2 и 3. Расстояние между скрещивающимися прямыми.

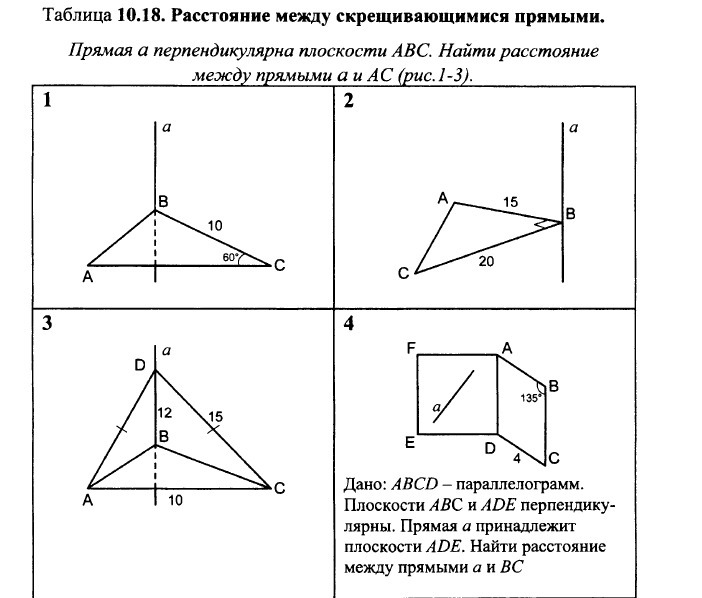
2. Расстояние между а и АС это перпендикуляр, опущенный из точки В на прямую АС.Узнав площадь треугольника АВС, сможем найти расстояние от а до АС.
S=AC*CB=15*20=300
S=AB*h⇒ 
AB*h=300⇒  h=300/AB
AB=√(AC²+CB²)=√(225+400)=25
h=300/25=12- расстояние от а до АС
3. ВС=√(DC²- DB²)=√(225-144)=9
AD=DC- по условию, как их проекции АВ=ВС , значит АВС-равнобедренный, высота, опущенная из В к АС будет являться также и  медианой, тогда
h=√(BC²-(1/2AC)²)=√(81-25)=√56=2√14 -расстояние от а до АС

Спасибо!!

Пожалуйста