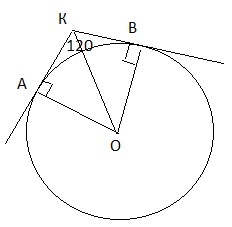
Прямі, які дотикаються до кола із центром О в точках А і В, перетинаються в точці К, кут АКВ дорівнює 120о. Доведіть, що АК + ВК = ОК.
50 баааааалллллллллллллоооооооооов

Насколько я поняла задачу, рисунок должен быть таким, как представлен в приложенном файле, тогда решение такое:
АК, ВК-касательные к окружности, по свойству касательных прямая КО является биссектрисой угла К, значит ∠ОКВ=120/2=60°,  ∠КОВ=90-60=30°, треугольник ОКВ-прямоугольный, значит гипотенуза равна двум катетам, лежащим против угла в 30 градусов.
ОК=2ВК, ВК=АК-как отрезки касательных, проведенных к окружности из одной точки. ⇒
АК+ВК=ОК