• Предмет: Геометрия
  • Автор: Lizochka0214
  • Вопрос задан 8 лет назад
< >

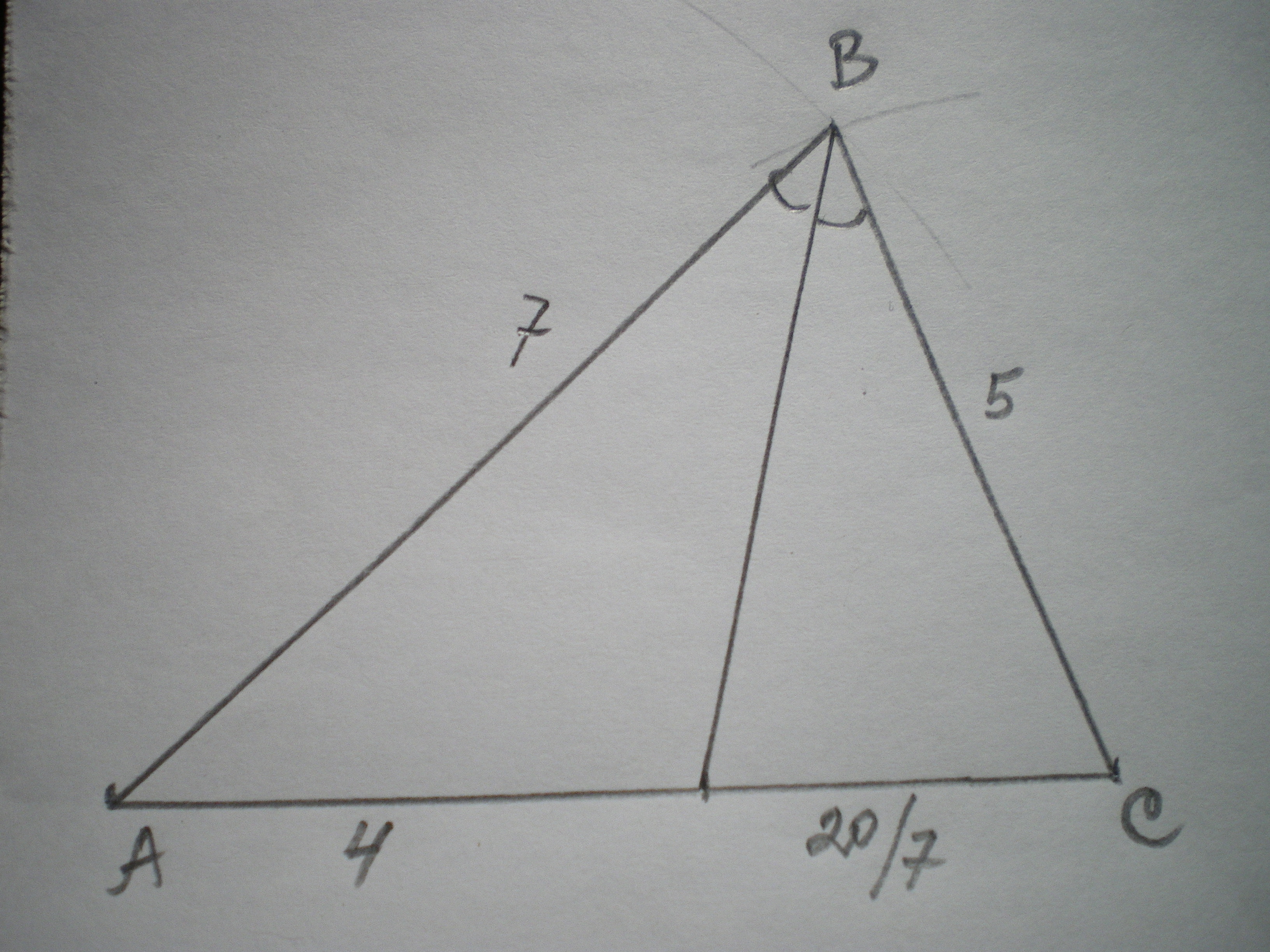
Из вершины B треугольника ABC опущена биссектриса BK. Найдите длину стороны BC, если AB=7,AK=4,KC=20/7

Ответы

Ответ дал: Пеппер
0

Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилегающим сторонам.

Отсюда соотношение сторон: АВВС=АККС

ВС=АВ*КС:АК

ВС=7*(207):4=5.

Ответ: ВС=5 ед.

Приложения:
Похожие вопросы
Английский язык
2 года назад
плииииииисссссссссссссссссссссс во мнч
Окружающий мир
2 года назад
кокое сегодня число ???
История
2 года назад
помогите плиз!!!! 1.Когда пресеклась династия Рюриковичей? 1. 1584 2. 1589 3. 1598 2. Кто был первым мужем Марины Мнишек? 1. Г. Отрепьев 2. "Тушинский Вор" 3. Б. Годунов 3.Отряды
Химия
2 года назад
Виберіть правильні твердження 1) Фізичні явища супроводжуються утворенням нових речовин, 2) Хімічне явище іє хімічною реакцією, 3)Кипіння води та утворення туману це і є хімічні явища 4) Під час
Математика
8 лет назад
1) пж - к обыкновенной дроби со знаменатилем 36 ток быстрее
Математика
8 лет назад
Решите пожалуйста. срочно нужно. 3-ее
Математика
9 лет назад
масштаб карты равен 1:50000.Определите растояние на местности если на карте оно равно 37 мм
Математика
9 лет назад
Решите пожалуйста уравнение 6*(3x-0,7)=4,8 спасибки))