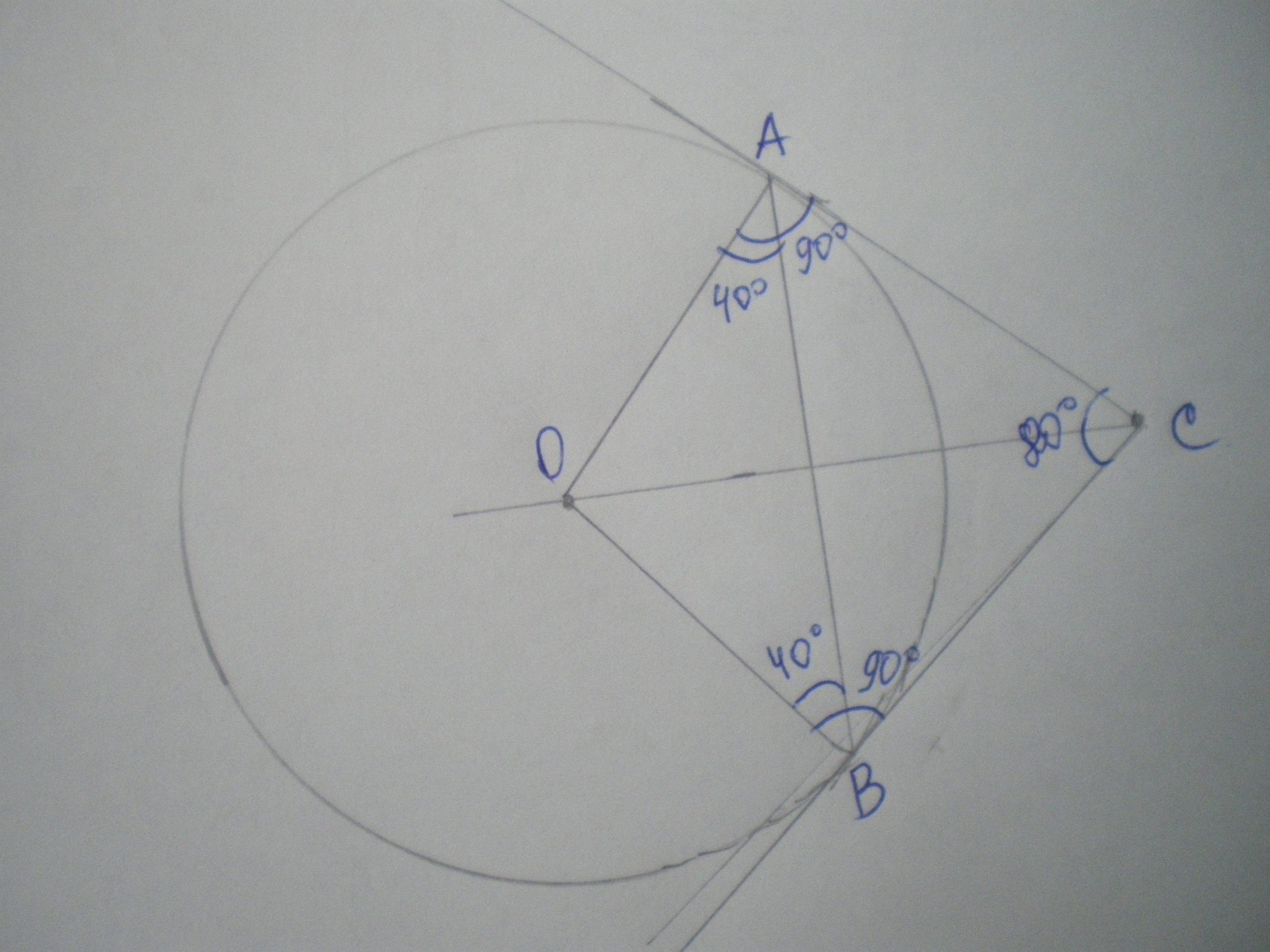
Две прямые касаются окружности с центром О в точках А и В и пересекаются в точке С. Найдите угол между этими прямыми, если 0 ∠ABO = 40 .

Рассмотрим треугольник АВС - равнобедренный, т.к. АС=ВС как касательный выходящие из одной точки.
Угол ОАС=углу ОВС=90 градусов по свойству касательной и радиуса окружности, значит, угол САВ=углу СВА=90-40=50 градусов
Угол АСВ=180-(50+50)=80 градусов.
Ответ: 80 градусов.