Предмет: Геометрия
Автор: итип
Вопрос задан 8 лет назад

Помогите решить, пожалуйста

Приложения:

Ответы

Ответ дал: Simba2017

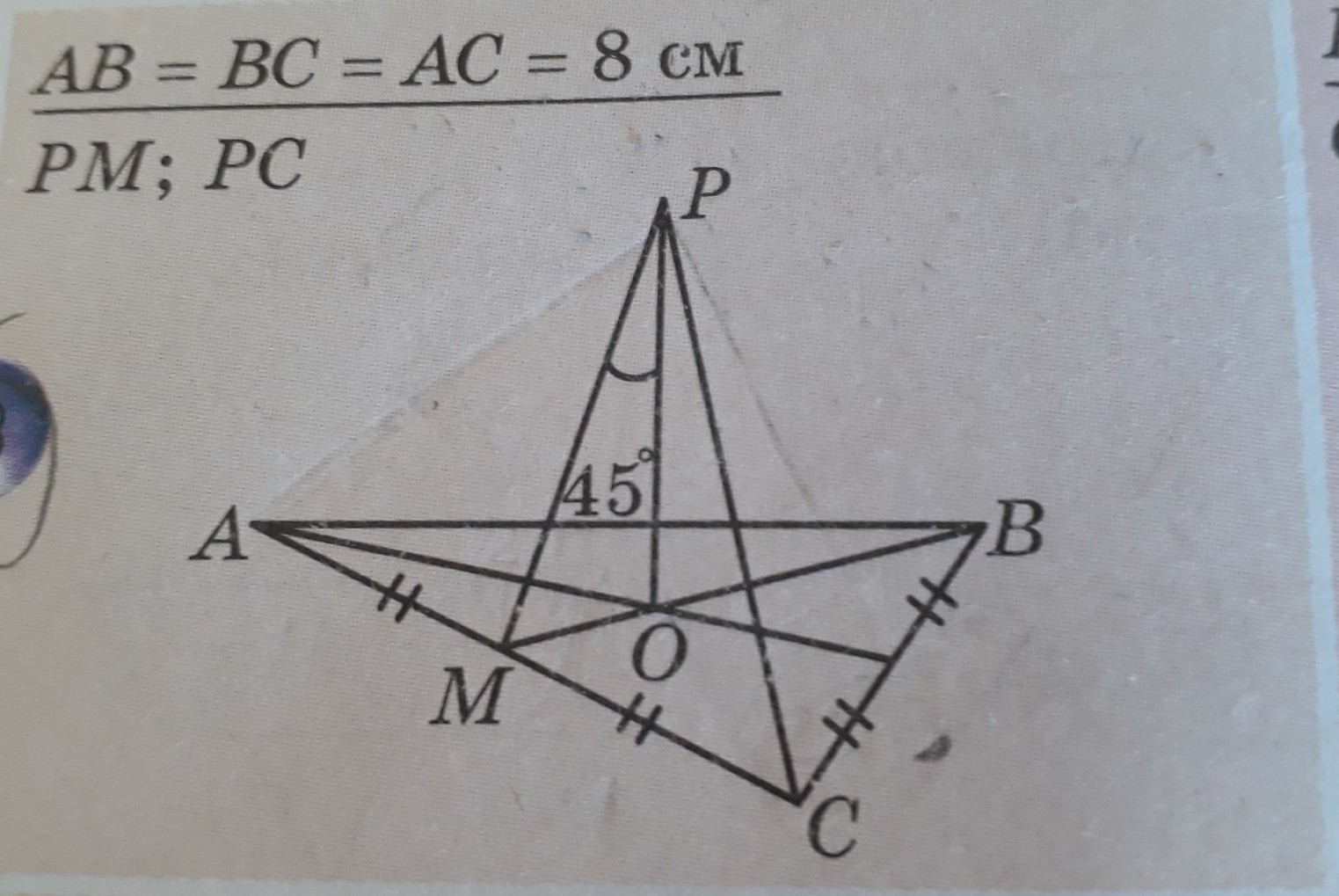
О-центр окружностей, делит медианы в отношении 2 к 1 от вершины
BM=CB*sin60=8*√3/2=4√3
BO=OC=OA=(2/3)*BM=8/√3
OM=BM/3=4/√3=PO
ΔOMP-равнобедренный и прямоугольный
MP=MO/sin45=4/√3/(√2/2)=4√(2/3)≈3.26
ΔPOC-прямоугольный
PC^2=PO^2+OC^2=(4/√3)^2+(8/√3)^2=16/3+64/3=80/3
PC=4√(5/3)≈5.16

Ответ дал: итип

Огромное спасибо

Ответ дал: xERISx

Задача имеет единственное решение только при условии, что PO перпендикулярно плоскости треугольника: PO⊥(ΔABC)

ΔABC - равносторонний: a = AB = BC = AC = 8 см
BM - высота, медиана и биссектриса
Точка О - точка пересечения биссектрис и высот - центр вписанной/описанной окружности для равностороннего треугольника
MO = r - радиус вписанной окружности
$MO = r = frac{a}{2 sqrt{3} } = frac{8}{2 sqrt{3} } =frac{4}{ sqrt{3} }$ см
AO = BO = CO = R - радиус описанной окружности
$CO = R = frac{a}{ sqrt{3} } = frac{8}{ sqrt{3} }$ см

ΔMOP - прямоугольный: ∠MOP=90°, ∠MPO = 45° ⇒
∠PMO = ∠MPO = 45° и PO = MO = $frac{4}{ sqrt{3} }$ ⇒
$PM = MO * sqrt{2} = frac{4}{ sqrt{3} } * sqrt{2} =4 sqrt{ frac{2}{3} }$ см

ΔCOP - прямоугольный: ∠COP = 90°. Теорема Пифагора
PC² = PO² + CO² =
$= (frac{4}{ sqrt{3} } )^2 + ( frac{8}{ sqrt{3} } )^2= frac{16}{3} + frac{64}{3} = frac{80}{3}$
$PC = sqrt{ frac{80}{3} } =4 sqrt{ frac{5}{3} }$ см

Ответ: $PM = 4 sqrt{ frac{2}{3} }$ см; $PC = 4 sqrt{ frac{5}{3} }$ см

Похожие вопросы

Русский язык

2 года назад

чем выражено дополнение,обстоятельство и определение?

Английский язык

2 года назад

Прошу помогите дам 50 даже 80баллов!!!!!!!!

История

2 года назад

які кочові племена починають походи на русь-україну у період правління ярославичів

География

2 года назад