Ответы
Ответ дал:
0
может я что то не понимаю но у меня получился такой ответ.
Приложения:
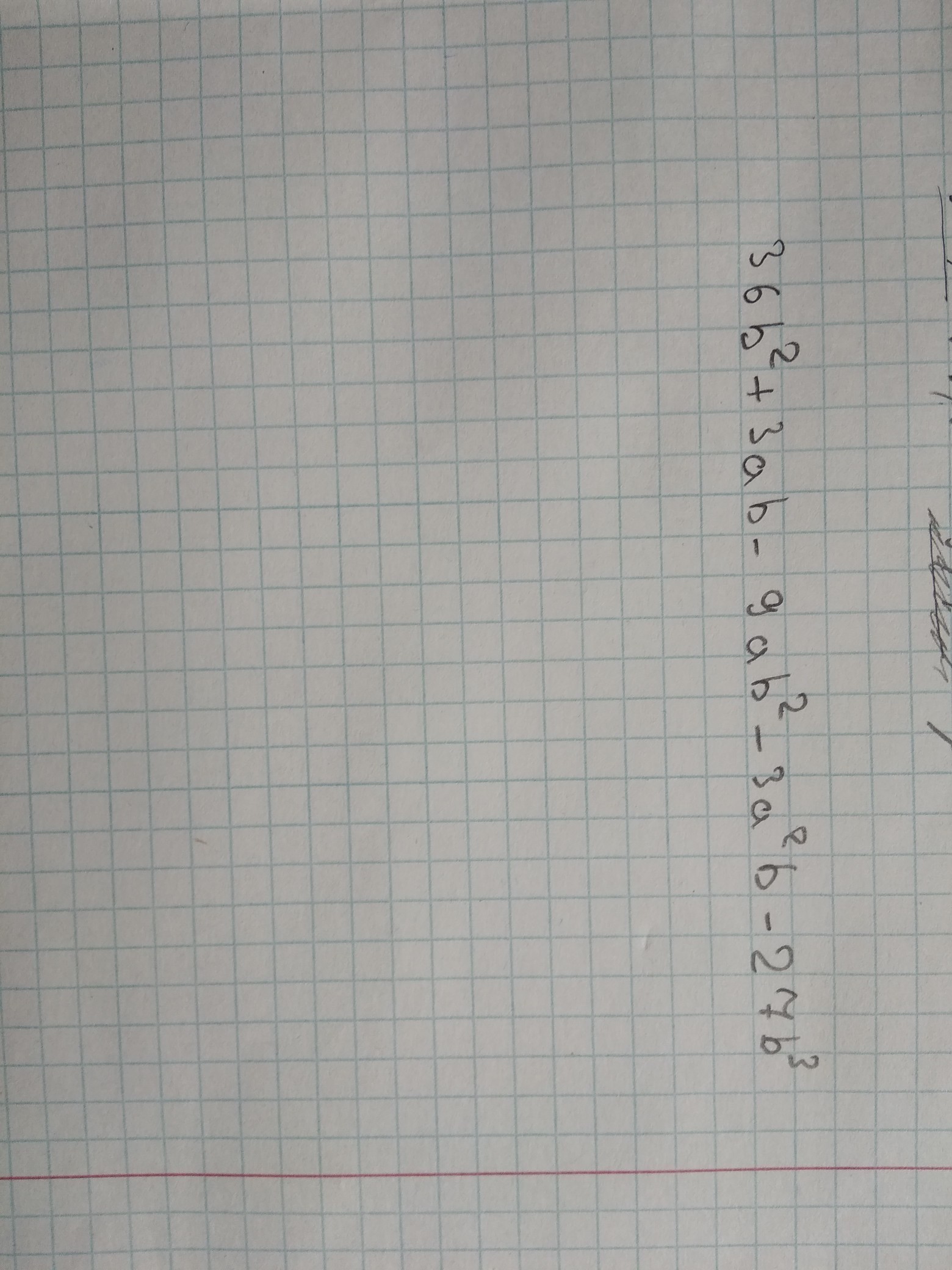
Ответ дал:
0
___ 3a^3 - 18b^3 =
= 3 * (a^3 - 9b^3) = 3 * [a^3 - (3b)^3] = 3 * (a - 3b)(a^2 + 3ab + 9b^2)
__ 18b^2*a + 6a^2*b + 2a^3 =
= 2a * (9b^2 + 3ab + a^2) = 2a * (a^2 + 3ab + 9b^2)
=> первая дробь будет:
[3 * (a - 3b)(a^2 + 3ab + 9b^2)] [2a * (a^2 + 3ab + 9b^2)] = 3(a-3b) 2a
__81a^2*b - 54ab^2 + 9b^3 =
= 9b * (9a^2 - 6ab + b^3) = 9b * (3a - b)^2
__ 2ab^2 - 12ba^2 + 18a^3 =
= 2a * (b^2 - 6ab + 9a^2) = 2a * (b - 3a)^2
=> вторая дробь будет:
[9b * (3a - b)^2] [2a * (b - 3a)^2] = 9b 2a
т. к. (3a - b)^2 = (b - 3a)^2, потому что
(3a - b)^2 = [(-1)*(3a - b)^2 = (-1)^2 * (3a - b)^2 = (3a - b)^2
Тогда сумма дробей будет:
3(a-3b) 2a + 9b 2a =
= (3a - 9b - 9b) 2a =
= 3a 2a = 32
= 3 * (a^3 - 9b^3) = 3 * [a^3 - (3b)^3] = 3 * (a - 3b)(a^2 + 3ab + 9b^2)
__ 18b^2*a + 6a^2*b + 2a^3 =
= 2a * (9b^2 + 3ab + a^2) = 2a * (a^2 + 3ab + 9b^2)
=> первая дробь будет:
[3 * (a - 3b)(a^2 + 3ab + 9b^2)] [2a * (a^2 + 3ab + 9b^2)] = 3(a-3b) 2a
__81a^2*b - 54ab^2 + 9b^3 =
= 9b * (9a^2 - 6ab + b^3) = 9b * (3a - b)^2
__ 2ab^2 - 12ba^2 + 18a^3 =
= 2a * (b^2 - 6ab + 9a^2) = 2a * (b - 3a)^2
=> вторая дробь будет:
[9b * (3a - b)^2] [2a * (b - 3a)^2] = 9b 2a
т. к. (3a - b)^2 = (b - 3a)^2, потому что
(3a - b)^2 = [(-1)*(3a - b)^2 = (-1)^2 * (3a - b)^2 = (3a - b)^2
Тогда сумма дробей будет:
3(a-3b) 2a + 9b 2a =
= (3a - 9b - 9b) 2a =
= 3a 2a = 32
Приложения:
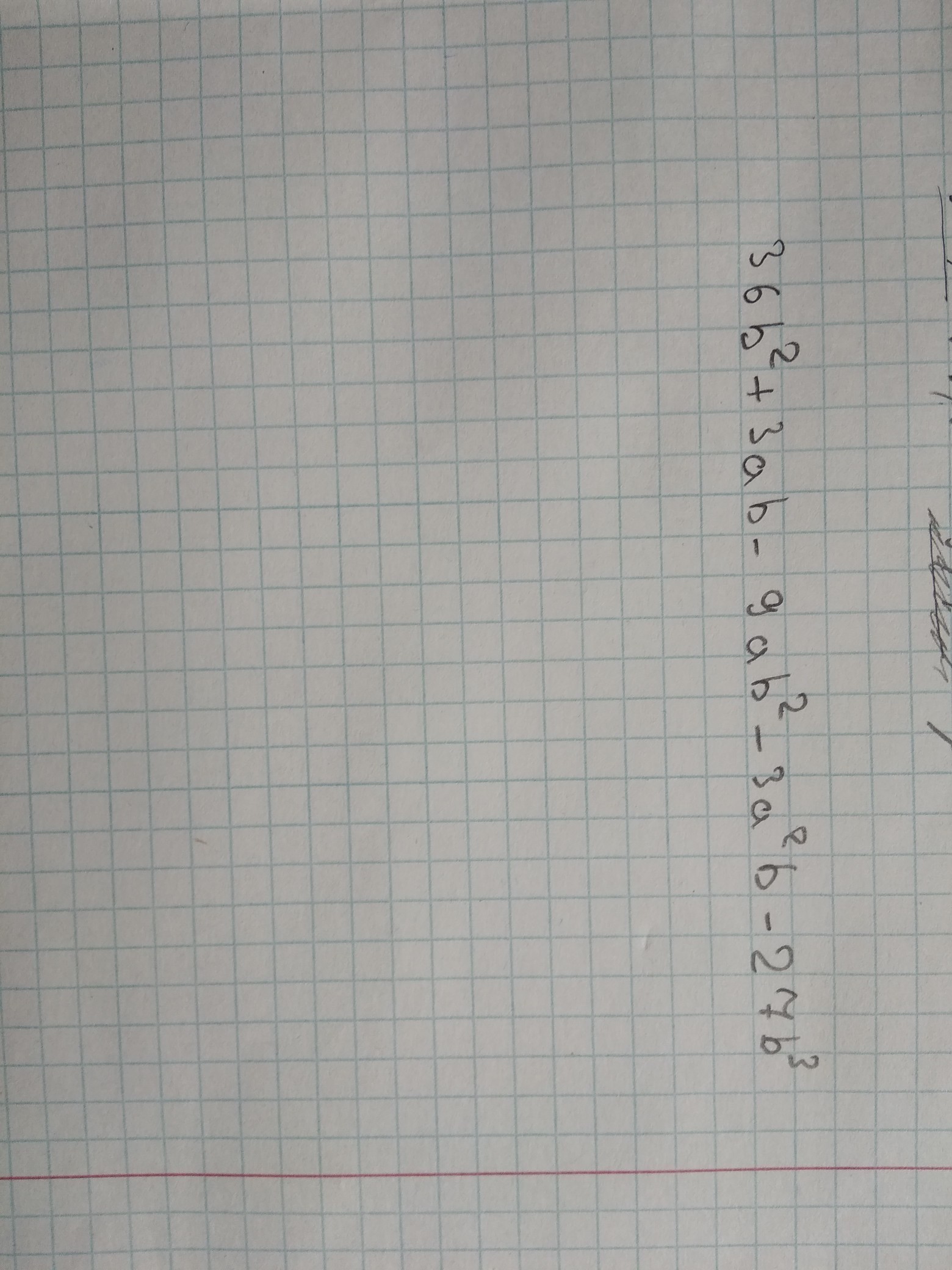
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад