В равнобедренном теугольнике с основанием АВ, угол А=углу АСВ+27°.Найдите Угол ВСD

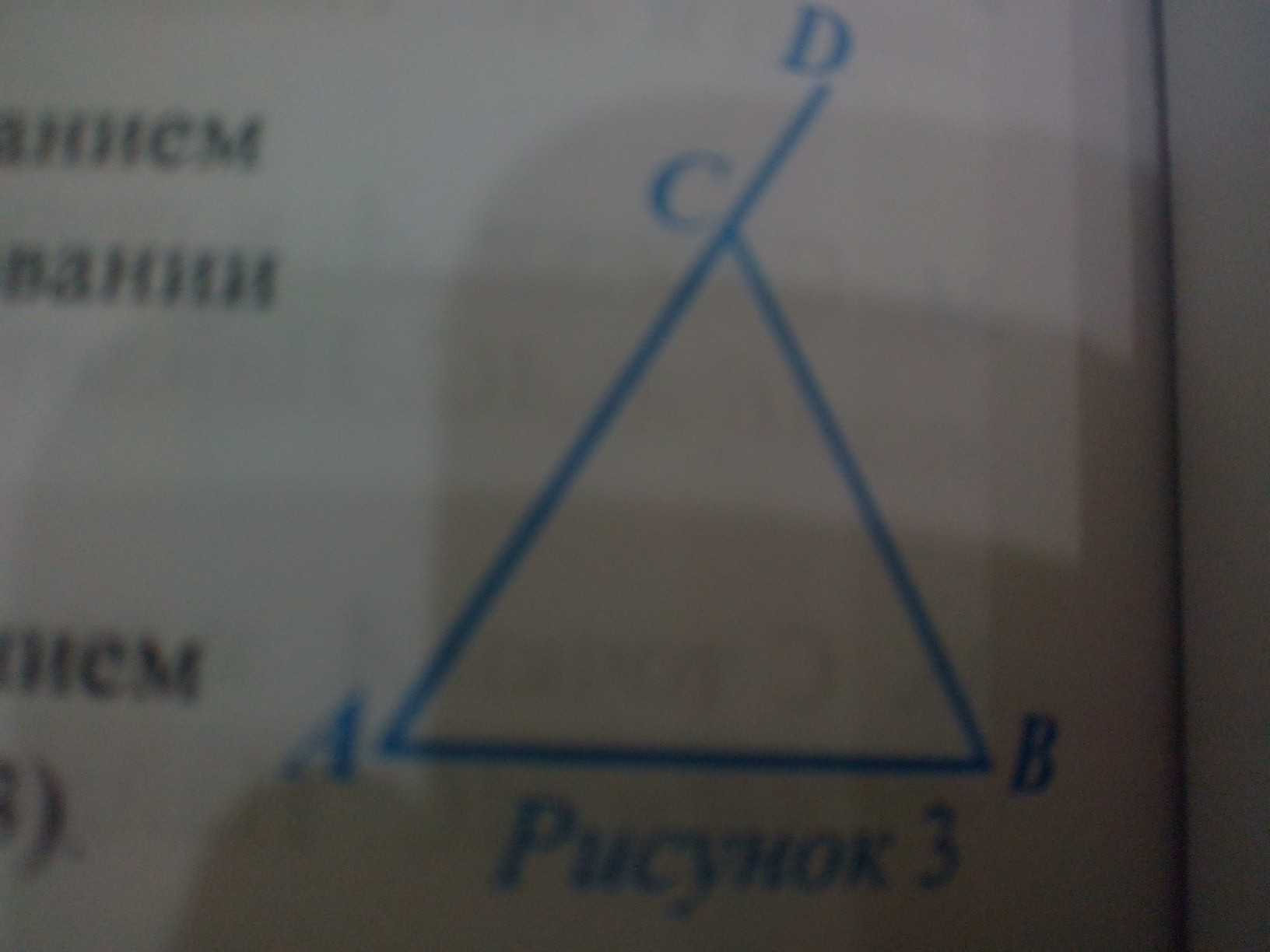
Дано:

 ∆АВС ;

АС = ВС;

<A = <B

 <А = <АСВ+27°

<ВCD - внешний

 Найти <ВСD

Решение.

1) Пусть <АCB = x

 тогда <A = <B = x + 27°

2) <BCD - внешний угол треугольника.

Внешний угол треугольника всегда равен сумме двух внутренних углов, не смежных с ним. 

Отсюда следует, что

< ВСD = <A + <B

Получаем

<BCD = x + 27°+ x + 27°

<BCD  = 2x + 54°

3) < ACB и  <BCD - смежные.

Сумма смежных углов равна 180°.

< ACB +  <BCD = 180°.

  х + 2х + 54° = 180°

            3х = 180°- 54°

             3x = 126°

              х = 126° : 3

               х = 42°

<ACB = 42°, тогда <BCD  = 2x + 54°

<BCD  = 2·42° + 54° = 84°+540= 138°

 Ответ: 138°.