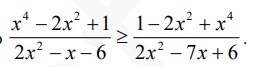Ответы
Ответ дал:
0
Решить неравенство

Решение
Числители обеих дробей равны
x⁴ - 2x² + 1 = (x² - 1)²
Следовательно при х = 1 и х = -1 числители данных неравенств равны нулю и неравенство истинно.
Знаменатели дробей раскладываем на множители
2x² - x - 6 = 0
D =(-1)² - 4*2*(-6) = 1 + 48 = 49


2x² - x - 6 = 2(x + 1,5)(x - 2) = (2x + 3)(x - 2)
2x² - 7x + 6 = 0
D = 7² - 4*2*6 = 49 - 48 = 1


2x² - 7x + 6 = 2(x - 1,5)(x - 2) = (2x - 3)(x - 2)
ОДЗ неравенства:х≠-1,5; x≠1,5; x≠2.
Запишем полученные выражения в исходное неравенство





Делим обе части неравенства на -6

Решаем методом интервалов
Находим точки где множители меняют свой знак
x₁ = -1,5 x₂ = 1,5 x₃ = 2
Наносим эти точки на числовую прямую и находим знаки левой части неравенства по методу подстановки.
Например при х=0

- + - +
------o----------o--------o-----------
-1,5 1,5 2
Следовательно решением неравенства являются
все значения х∈[-∞;-1,5)U{-1}U{1}U(1,5;2)
Ответ: х∈[-∞;-1,5)U{-1}U{1}U(1,5;2)
Решение
Числители обеих дробей равны
x⁴ - 2x² + 1 = (x² - 1)²
Следовательно при х = 1 и х = -1 числители данных неравенств равны нулю и неравенство истинно.
Знаменатели дробей раскладываем на множители
2x² - x - 6 = 0
D =(-1)² - 4*2*(-6) = 1 + 48 = 49
2x² - x - 6 = 2(x + 1,5)(x - 2) = (2x + 3)(x - 2)
2x² - 7x + 6 = 0
D = 7² - 4*2*6 = 49 - 48 = 1
2x² - 7x + 6 = 2(x - 1,5)(x - 2) = (2x - 3)(x - 2)
ОДЗ неравенства:х≠-1,5; x≠1,5; x≠2.
Запишем полученные выражения в исходное неравенство
Делим обе части неравенства на -6
Решаем методом интервалов
Находим точки где множители меняют свой знак
x₁ = -1,5 x₂ = 1,5 x₃ = 2
Наносим эти точки на числовую прямую и находим знаки левой части неравенства по методу подстановки.
Например при х=0
- + - +
------o----------o--------o-----------
-1,5 1,5 2
Следовательно решением неравенства являются
все значения х∈[-∞;-1,5)U{-1}U{1}U(1,5;2)
Ответ: х∈[-∞;-1,5)U{-1}U{1}U(1,5;2)
Ответ дал:
0
последнюю строчку проверьте Ответ: х∈[-∞;-1,5)U{1}U{1}U(-1,5;2), ОПЕЧАТКИ
Ответ дал:
0
ДОЛЖНО БЫТЬ х∈[-∞;-1,5)U{-1}U{1}U(1,5;2)
Ответ дал:
0
исправил
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад