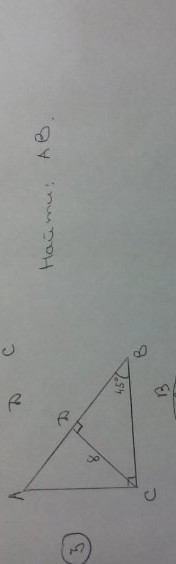Ответы
Ответ дал:
0
Вариант решения.
На рисунке треугольник АВС - прямоугольный, его высота из прямого угла СD=8, угол СВА=45°
Сумма острых углов прямоугольного треугольника 90°, поэтому второй острый угол равен 45°. ⇒
По равенству двух углов этот треугольник равнобедренный и СD - его биссектриса и медиана.
Медиана равнобедренного прямоугольного треугольника равна половине гипотенузы. ⇒
АD=DB=CD=8.
АВ=AD+DB=16 ( ед. длины)
На рисунке треугольник АВС - прямоугольный, его высота из прямого угла СD=8, угол СВА=45°
Сумма острых углов прямоугольного треугольника 90°, поэтому второй острый угол равен 45°. ⇒
По равенству двух углов этот треугольник равнобедренный и СD - его биссектриса и медиана.
Медиана равнобедренного прямоугольного треугольника равна половине гипотенузы. ⇒
АD=DB=CD=8.
АВ=AD+DB=16 ( ед. длины)
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад