Дано:окр. (О, r)-вписанная в треугольник ABC, угол C=90 градусов, r=2, AB=10
Найдите периметр треугольника ABC
Приложения:
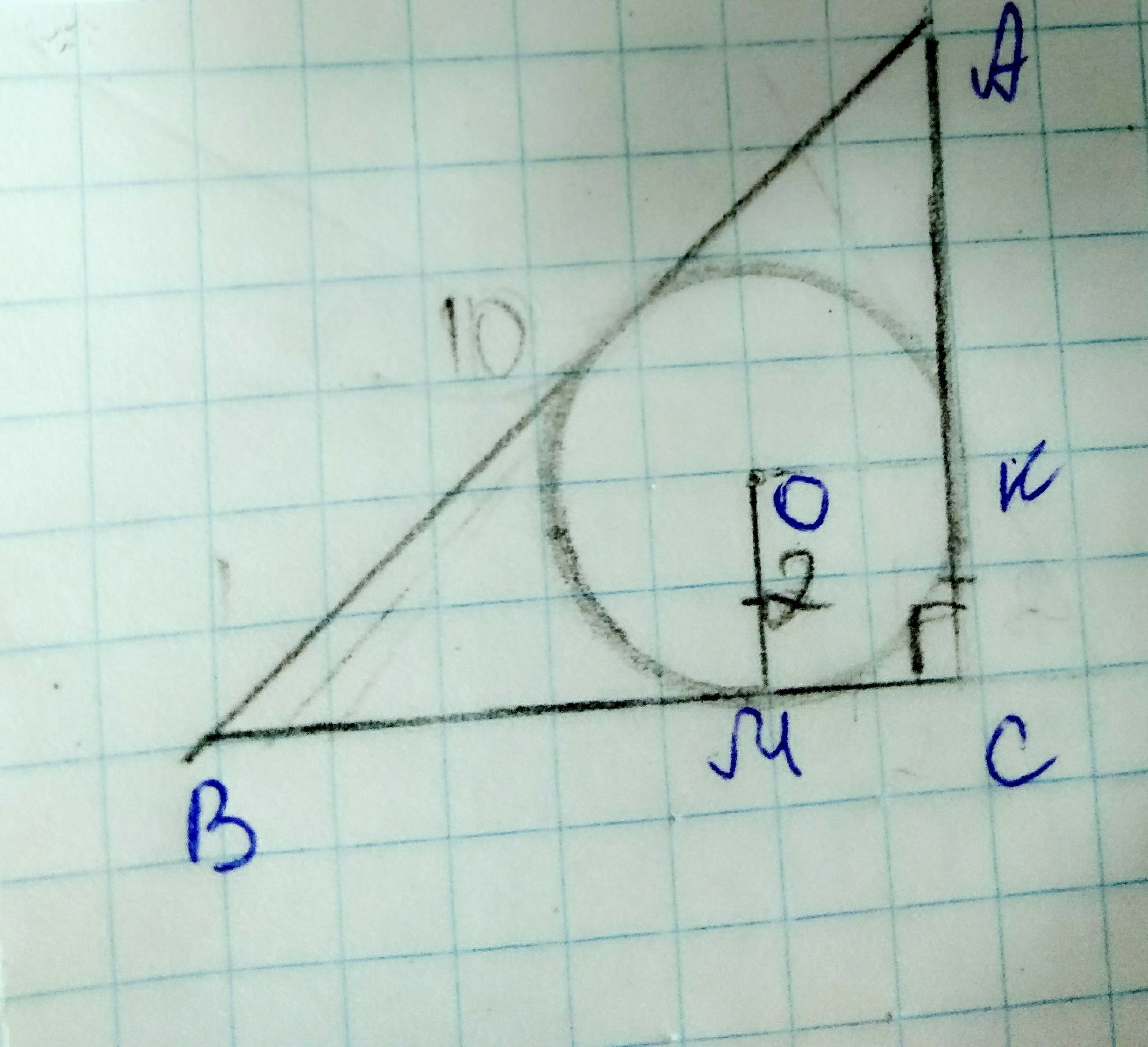
Ответы
Ответ дал:
0
Проведем OH ⊥AB HB=x AH=10-x
(x+10-x)^2=(10-x+2)^2+(2+x)^2
100=64-16x+x^2+4+4x+x^2
0=2x^2-12x-32
x^2-6x-16=0
x1=8 x2=-2(не подходит)
AC=4 BC=10 AB=10 P=24 ,но такого треугольника не может быть
(x+10-x)^2=(10-x+2)^2+(2+x)^2
100=64-16x+x^2+4+4x+x^2
0=2x^2-12x-32
x^2-6x-16=0
x1=8 x2=-2(не подходит)
AC=4 BC=10 AB=10 P=24 ,но такого треугольника не может быть
Ответ дал:
0
Спасибо))
Ответ дал:
0
Ой ,ошибся ,100=144-24x+x^2+4+4x+x^2 x^2-10x+24=0 x1=4 x2=6 P=6+8+10=24
Ответ дал:
0
Т.е треугольник все таки существует?
Ответ дал:
0
Да стороны
Ответ дал:
0
существует и заметьте что в задании не требуется находить его стороны, а только периметр
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад