Предмет: Математика
Автор: 112017
Вопрос задан 8 лет назад

< >

а) вычислить интеграл используя непосредственное интегрирование и основные свойства интегрирования;
б) вычислить интеграл методом подстановки.

Приложения:

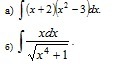
Ответы

Ответ дал: NNNLLL54

0

$1); ; int (x+2)(x^2-3), dx=int (x^3-3x+2x^2-6), dx=\\=frac{x^4}{4}-3cdot frac{x^2}{2}+2cdot frac{x^3}{3}-6x+C\\2); ; int frac{x, dx}{sqrt{x^4+1}}=int frac{x, dx}{sqrt{(x^2)^2+1}}=[, t=x^2; ,; dt=2x, dx, ]=\\=frac{1}{2}int frac{dt}{sqrt{t^2+1}}=frac{1}{2}cdot ln|x+sqrt{t^2+1}|+C=frac{1}{2}cdot ln|x^2+sqrt{x^4+1}|+C$

Похожие вопросы

Русский язык

2 года назад

морфемный разбор слова придаёт 5 класс

Русский язык

2 года назад

звуко-буквенный разбор слова свежие

Английский язык

2 года назад

Срочно!!! Английский, времена

Оʻzbek tili

2 года назад

Смотря на этот рисунок составьте сочинение про Навруз

Математика

8 лет назад

Сторона основания правильной 4-угольной пирамиды равна 9√2, боковое ребро равно 13 см. Найти периметр и площадь диагонального сечения и апофему.

Математика

8 лет назад

Хватит ли плинтуса 21 м для ремонта комнаты прямоугольной формы, размеры которой 4м и 5м?Ответ обоснуй решением!

Алгебра

9 лет назад

Запишите в виде выражения: утроенное произведение разности чисел а и б и их суммы

Математика

9 лет назад

В посылку можно положить груз массой не более 10кг.Выберите по массе грузы,которые можно положить в одну посылку: 1)4кг 400г и 3кг 600г; 2)6кг 200г и 5кг 600г; 3)4кг 600г и 7кг 700г; 4)6кг 100г и