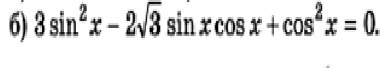Предмет: Алгебра
Автор: comsasha2018
Вопрос задан 8 лет назад

Надеюсь на вашу помощь. Даю 40 балов, спасибо*

Приложения:

Ответы

Ответ дал: 999Dmitry999

$3sin^2(x)-2 sqrt{3} sin(x)cos(x)+cos^2(x)=0\3sin^2(x)-2sqrt{3} sin(x)sqrt{1-sin^2(x)} +1-sin^2(x)=0\sin(x)=t$
t∈[-1;1]
$3t^2-2sqrt{3} t sqrt{1-t^2} +1-t^2=0\3t^2-2tsqrt{3-3t^2} +1-t^2=0\-2tsqrt{3-3t^2} =-2t^2-1\4t^2(3-3t^2)=4t^4+4t^2+1\12t^2-12t^4-4t^4-4t^2-1=0\-16t^4+8t^2-1=0\-(16t^4-8t^2+1)=0\-(4t^2-1)^2=04t^2-1=0\t^2= frac{1}{4} \t= frac{1}{2} \t= -frac{1}{2} \3( frac{1}{2} )^2-2 sqrt{3} * frac{1}{2} * sqrt{1-( frac{1}{2})^2 } +1-( frac{1}{2} )^2= frac{3}{4} - sqrt{3} * frac{ sqrt{3} }{2}+ frac{3}{4} = frac{3}{4} - frac{3}{2} +\+ frac{3}{4} =0$
$3(- frac{1}{2} )^2-2 sqrt{3} (- frac{1}{2} ) sqrt{1-(- frac{1}{2})^2 } +1-(- frac{1}{2} )^2= frac{3}{4} + sqrt{3(1- frac{1}{4} )} +1- frac{1}{4} \= frac{3}{4} + sqrt{ frac{9}{4} } +1- frac{1}{4} =3\3 neq 0\sin(x)= frac{1}{2} \x=(-1)^k frac{pi}{6} +pi k$
k∈Z

Ответ дал: mmb1

3sin²(x) - 2√3sin(x)*cos(x) + cos²(x) = 0
(√3sin(x))² - 2*(√3sin(x))*cos(x) + (cos(x))² = 0
(√3sin(x) - cos(x))² = 0
√3sin(x)=cos(x)
если cos(x)=0 то sin(x)≠0 и решений нет, значит cos(x) не равен 0 и можно обе части поделить на cos(x)
√3tg(x)=1
tg(x)=1/√3=√3/3
x=π/6 + πn n∈Z

Похожие вопросы

Русский язык

2 года назад

из -за невнимательности была допущена досадная ошибка в контрольной работе. чем выражена обстоятельство

Русский язык

2 года назад

как проверить букву т в слове ИзвесТно,как проверить букву а в слове рАскрываются,как проверить букву е в слове бабочЕк,что за часть речи слово если,что за часть речи слово жди.

Қазақ тiлi

2 года назад

Помогите все вопросы 10 пожи

Қазақ тiлi

2 года назад