На окружности по разные стороны от диаметра AB взяты точки M и N. Известно что NBA 71
Найдите NMB

Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр. /NBA является вписанным в окружность углом, следовательно (по теореме о вписанном угле) дуга AN равна 71°*2=142. Тогда дуга NB равна 180°-142°=38 /NMB - тоже вписанный в окружность, следовательно он равен 38/2=19° Ответ:19

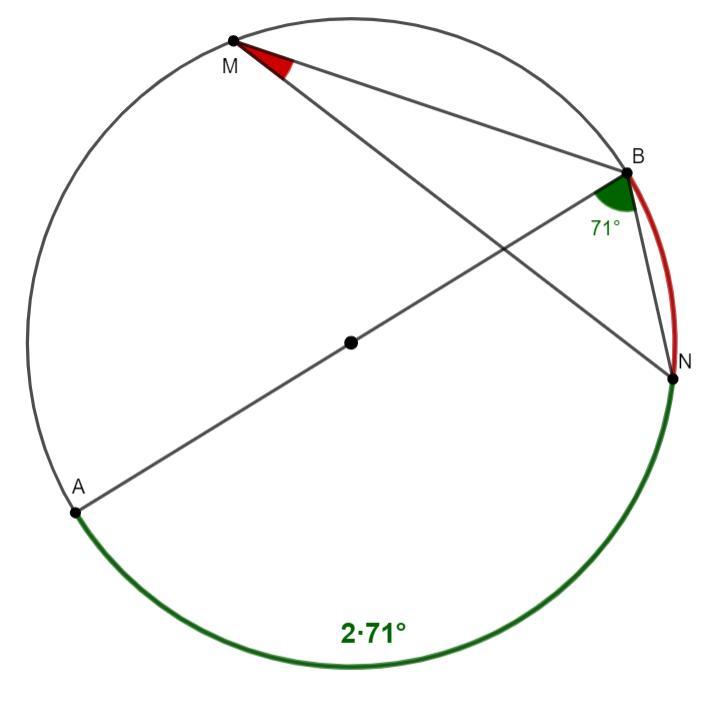
Вписанный угол опирающийся на дугу, вдвое меньше её. Поэтому:

∪AN=2·∠NBA=2·71°=142° и ∠NMB=∪NB:2.

∪AB=180°, как полуокружность.

∪NB=∪AB-∪AN=180°-142°=38°

∠NMB=∪NB:2=38°:2=19°

Ответ: 19°.

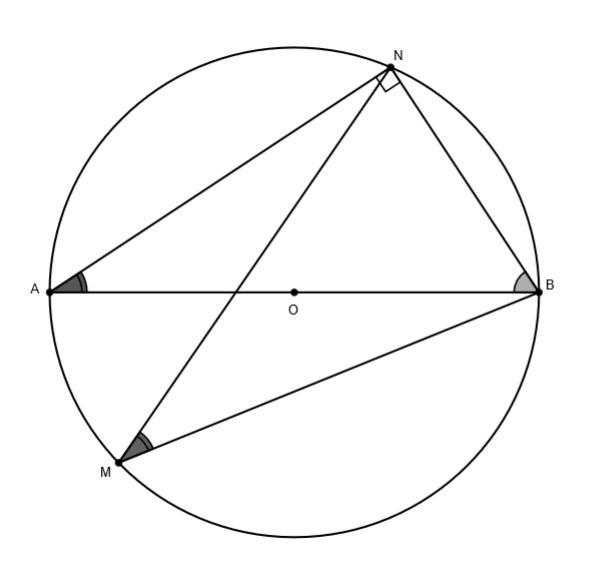
Теорема 1:  Вписанный угол, опирающийся на диаметр окружности, прямой

∠ANB = 90⁰ - опирается на диаметр АВ

∠NAB = 180⁰ - 90⁰ - 71⁰ = 19⁰ - третий угол Δ ABN

Теорема 2:  Вписанные углы, опирающиеся на равные дуги, равны

∠NAB = ∠NMB = 19⁰ - опираются на общую дугу NB