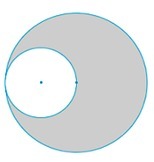
Две окружности касаются, причем меньшая из окружностей проходит через центр большей окружности (см. рисунок). Найдите площадь закрашенной фигуры (в см2), если меньшая из окружностей ограничивает круг площадью 64 см2.

Исходя из рисунка, можно сделать вывод, что диаметр меньшего круга - радиус большего. Находим радиус большего круга по формуле площади (

А именно

Так мы нашли диаметр малого круга (8см)
затем поделим на 2 и получим радиус 4см
Найдем площадь малого круга -

Чтобы получить площадь закрашенной области, отнимем от площади большего круга площадь меньшего:

это и есть наш ответ.