Диагонали выпуклого четырехугольника равны a и b, угол между ними 45°. Найдите отрезки, соединяющие середины противолежащих сторон четырехугольника

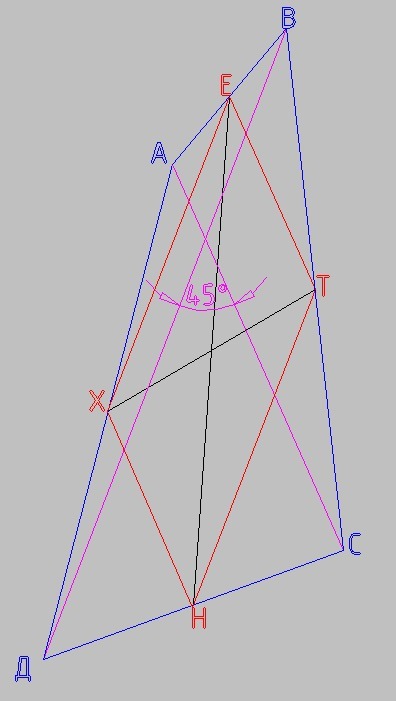
a = AC
в = ВД
l₁ = ЕН
l₂ = ХТ
ЕТ - средняя линия треугольника АВС
ЕТ = а/2
Аналогично
ХН = а/2
ТН = ЕХ = в/2
Эти среднии линии параллельны диагоналям и углы между средними линиями совпадают с углами между диагоналями, меньший 45° и больший 135°
По теореме косинусов для треугольника ЕТН
ЕН² = ЕТ² + ТН² - 2*ЕТ*ТН*cos(135°)
l₁² = (a/2)² + (b/2)² + 2*(a/2)*(b/2)*cos(45°)
l₁² = a²/4 + b²/4 + a*b/(2√2)
l₁² = 1/4(a² + b² + a*b√2)
l₁ = 1/2√(a² + b² + a*b√2)
аналогичное уравнение для треугольника ЕХТ
l₂² = (a/2)² + (b/2)² - 2*(a/2)*(b/2)*cos(45°)
l₂ = 1/2√(a² + b² - a*b√2)

Спасибо